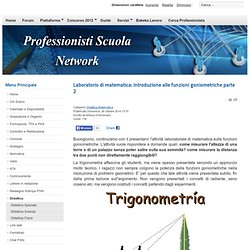
Come realizzare esperienze scientifiche quando il laboratorio non c’è….. – La Fucina delle Scienze. Come realizzare esperienze scientifiche quando il laboratorio scientifico non c’è… di Alfonso D’Ambrosio , docente di Matematica e Fisica IIS Cattaneo Mattei, Monselice (Pd) In un tweet: esperimenti reali a casa e a scuola con lo smartphone Destinatari: Docenti e studenti Tipologia di scuola a cui è diretto: Secondaria di I e II grado Introduzione.
Quante sono le geometrie? Risposte ad un lettore. Il nostro lettore FABRY2 ci scrive in un commento: "Ho letto in un libro (divulgativo) che in dimensione 3 ci sono "otto diversi tipi di geometrie".

Camiciottoli2. 585032main Geom ED Full Circle. Missing square puzzle - Wikipedia. Missing square puzzle animation, like a "magician presentation.
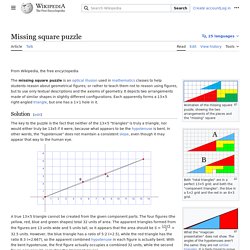
" Both "total triangles" are in a perfect 13×5 grid; and both the "component triangles", the blue in a 5×2 grid and the red in an 8×3 grid. The missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures; or rather to teach them not to reason using figures, but to use only textual descriptions and the axioms of geometry.
It depicts two arrangements made of similar shapes in slightly different configurations. Each apparently forms a 13×5 right-angled triangle, but one has a 1×1 hole in it. Euclid: The Game - Tutorial. Bergamo in un quadro di Escher? No, la magia è in queste foto - Bergamo città Bergamo. Rete di Eratostene. 593843main ALG ED SuitYourself final. Eratosthenes Experiment 2015. Quando il soffitto è un capolavoro: dieci modelli di volta. Dopo aver presentato i dieci modelli di arco più diffusi è arrivato il momento di conoscere il meraviglioso mondo delle volte.
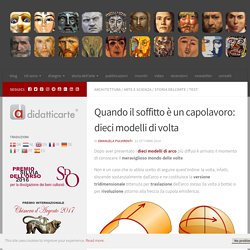
Non è un caso che io abbia scelto di seguire quest’ordine: la volta, infatti, discende sostanzialmente dall’arco e ne costituisce la versione tridimensionale ottenuta per traslazione dell’arco stesso (la volta a botte) o per rivoluzione attorno alla freccia (la cupola emisferica). Distanza euclidee e non: la proposta francese di andare al lavoro in bici, i tassisti e il concetto matematico di distanza. Qualche giorno fa, chiacchierando con alcuni colleghi in ufficio la discussione è presto caduta su una nuova legge approvata dal parlamento Francese su invito del ministro dell'economia d'oltralpe Ségolèn Royal.
In breve, la legge prevede un rimborso monetario da parte delle aziende ai loro dipendenti che si recano a lavoro in bicicletta in funzione della distanza percorsa. Dopo un attimo di esitazione, quasi contemporaneamente, a tutti è balenata in mente la stessa domanda “Come viene calcolata la distanza percorsa?” Cerruti_prog_49.pdf. Crucinumero_circonferenza.pdf. Il pentagono tra geometria ed arte. Alchimia, biologia, esoterismo e matematica.
Tutti mescolati dentro un grande calderone di forma pentagonale, una figura che da millenni è stata caricata di ogni simbolismo possibile. Ma non è un caso: il pentagono, infatti, presenta delle proporzioni molto particolari che hanno solleticato l’immaginazione di filosofi, artisti e scienziati. Geometria senza curve - guida poligonale geogebricamente assistita. "Si capiscono davvero solo le cose che si è capaci di costruire" Gianbattista Vico E’ il vecchio discorso sulla teoria e la pratica, lo sporcarsi le mani mentre il cervello suda, il concretizzare le conoscenze in qualcosa di tangibile, la scuola completamente scollegata con il mondo reale, il mondo che c’è la fuori, il mondo del lavoro, quello che domani dovrebbe garantirci la pagnotta.

C’è questo processo formativo consolidato secondo il quale si prende il cranio di uno studente e lo si riempie di nozioni spesso astratte (almeno così da alcuni vengono percepite); è un procedura unilaterale di trasferimento di conoscenze nozionistiche tra docente e studente. Inganni spaziali e illusioni ottiche. Ricordate i nove indizi di profondità di cui ho già parlato?
Ebbene, si tratta di meccanismi percettivi talmente radicati nel nostro cervello che, nel momento in cui qualche elemento nel campo visivo ne contraddice le regole, non siamo più in grado di stabilire distanze, orientamento o dimensioni degli oggetti osservati. Il nostro sistema visivo, infatti, da un lato si aspetta che gli oggetti lontani appaiano più piccoli di quelli vicini, da un altro lato sa che, a dispetto di tale diversità percepita, gli oggetti non cambiano realmente dimensione o forma (caratteristica definita costanza percettiva) solo perché sono lontani o sono visti di scorcio, e continua a vederli come dovrebbero essere e non come effettivamente li vede.
How to Create Concentric Circles, Ellipses, Cardioids & More Using Straight Lines and a Circle. How to Create Concentric Circles, Ellipses, Cardioids & More Using Straight Lines and a Circle Using only a circle and straight lines, it's possible to create many different curves that are quite pleasing to look at and well known mathematically.
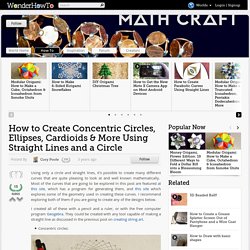
Most of the curves that are going to be explored in this post are featured at this site, which has a program for generating them, and this site which explores some of the geometry used in creating these curves. I recommend exploring both of them if you are going to create any of the designs below. I created all of these with a pencil and a ruler, or with the free computer program Geogebra. Laboratorio di matematica: introduzione alle funzioni goniometriche parte 2. Dettagli Categoria: Didattica Matematica Pubblicato Domenica, 26 Ottobre 2014 13:15.