

Twitter. Twitter. Twitter. Twitter. Twitter. Flexibility with Place Value. Just a quick post about place value and how important it is for students to be able to decompose numbers by place value in different ways.
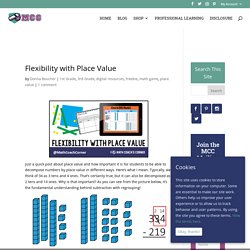
Here’s what I mean. Typically, we think of 34 as 3 tens and 4 ones. That’s certainly true, but it can also be decomposed as 2 tens and 14 ones. Why is that important? As you can see from the picture below, it’s the fundamental understanding behind subtraction with regrouping! Kiddos need lots of hands-on practice decomposing numbers in different ways. Twitter. Twitter. Twitter. Inaba’s Place Value Puzzles: Making Connections and Asking “What If” – Embrace the Challenge. Last week, my sixth graders helped me make connections between a puzzle I used in third grade and their current work with place value, specifically multiplying and dividing by powers of ten.
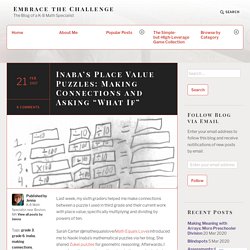
Sarah Carter (@mathequalslove/Math Equals Love) introduced me to Naoki Inaba’s mathematical puzzles via her blog. She shared Zukei puzzles for geometric reasoning. Afterwards, I saw a few other people posting about other puzzles by Inaba. (Apparently some have even been featured in the NYT… I feel so behind the times!) On Inaba’s website, I found a puzzle Google Translate identified as “Zero Zero Expression,” I suppose because it involves zeroes…? The original puzzles (found here) gives a series of one digit numbers and a sum, and asks the student to multiply the one digit numbers by 1, 10 or 100 to balance the equation.
Place Value-Building Meaning Behind the Numbers. Place value is such a fundamental concept, and it’s very difficult for kiddos to understand. Let’s think about the typical place value progression: Kindergarten–Understanding the meaning of numbers from 11-19. Double ten-frames are a great tool, as students see, for example, that 12 is a full ten-frame and 2 more. The ten-frames become a very visual representation of tens and ones.1st Grade–Students explore 2-digit numbers and understand that the two digits represent quantities of tens and ones. Beginning with the ten-frames provides a familiar context for students. The Difference Between Knowing and Understanding Place Value. My 2nd graders have been exploring place value, so yesterday I wrote the number 43 on the table in front of one sweet friend and asked what he could tell me about the number 43. He proudly told me it was 4 tens and 3 ones.
This is very common, right? We ask students to name the place value positions or tell us what digit is in the tens place, etc. I handed him a student ten-frame kit and asked him to build the number 43 using ten-frames. He immediately reached for a 4 tile. Flexibility with Place Value. New standards call for an increased emphasis on understanding place value, rather than just, for example, identifying the digit in a certain place value position (eg., In the number 345, what digit is in the hundreds place?).
In Texas, both the 1st and 2nd grade TEKS contain wording that indicates students should be able to think flexibly about place value. 1.2.B Use concrete and pictorial models to compose and decompose numbers up to 120 in more than one way as so many hundreds, so many tens, and so many ones 2.2.A Use concrete and pictorial models to compose and decompose numbers up to 1,200 in more than one way as a sum of so many thousands, hundreds, tens, and ones.
Number Disks: A great way to visualize the operations – The Other Math. Recently, I have found myself vociferously advocating for more teachers to use number disks when teaching the four operations of whole numbers: addition, subtraction, multiplication, and division.
Clearly my excitement for number disks has not yet rubbed off onto all the teachers I work with, because today I received the following question: Why are disks better than the 100 blocks, ten sticks, and ones cubes we have been using? It is clear the teacher is a user of Base 10 blocks. It is reasonable to ask why, if Base 10 blocks work, then why should we also learn about number disks. Expanded Form vs Expanded Notation. Among all the tsunami-force changes that took place as we moved to our new elementary TEKS (Texas Essential Knowledge and Skills) last year, one rather subtle shift might have been overlooked.
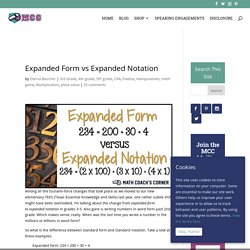
I’m talking about the change from expanded form to expanded notation in grades 3-5. Also gone is writing numbers in word form past 2nd grade. Which makes sense, really. When was the last time you wrote a number in the millions or billions in word form? What visual representations have folks been using to help kiddos understand that each position to the right in base ten is 1/10 of the the position to the left? @BerkeleyEverett Other than @ExplodingDots ? EJ891799. Teaching for Deep Understanding. Flexibility with Place Value. Decomposing PV Puzzles Freebie.pdf. Down the Rounding Rabbit Hole. Rounding has always been difficult for me to teach, and I suspect I'm not alone.
Here's a look at some of the many gimmicks, tricks, and tools teachers have used in an effort to get this concept across: Our curriculum likes number lines: I've spent more time than usual this fall thinking about rounding; both the why and the when, but also simply the how. Using a number line to round is all well and good, but it's not going to help you solve these problems... ...unless you can do the following: Identify place value locations and the value of the digit in a given place value.Identify the next multiple in that place value.Find the halfway point between the two multiples to use as a benchmark.Decide whether the number is more or less than halfway. That's one big cognitive load. Last year, I tried something different with some third graders who were having difficulty with rounding. And this: without the board or the arrow cards, I moved her on to rounding. ITP Moving Digits - Mathsframe.
I am remaking the ITPs so that they will work on all modern browsers and tablets.

They will remain freely available to all without the need for a subscription. View full screen in your browser. This ITP allows you to demonstrate the effect of multiplying and dividing by 10 and 100. By dragging cards from the set of digit cards, different decimal numbers can be displayed. These decimal numbers can be placed in either of the two middle rows. Place Value-Building Meaning Behind the Numbers. Small Change, Big Difference part 1. Why you should eliminate 'POINT' from your vocabulary. - Sara VanDerWerf. Hello my friends. we are moments away from the start of 2019.

When you return to your classrooms this January it is difficult to make big changes to your classroom culture (these work best at the start of the school year), but NOW is the perfect time to implement small changes. Models for Initial Decimal Ideas - National Council of Teachers of Mathematics. EJ891799. The Difference Between Knowing and Understanding Place Value. What Does a Million Look Like? The United States is known for its culture of achievement around math.
In Mathematical Mindsets, Jo Boaler discusses the toxicity of this achievement culture, which she says disincentivizes teachers from using open-ended tasks that allow for multiple pathways to plausible solutions—instead they opt for more reliable means for approaching math, usually in the form of workbooks and worksheets. In reality, though, math is a literacy, and it’s important that it be treated as such. It’s reductive to teach it only through simple call-and-response questions. Math requires curiosity, inquiry, and, most importantly, play. In an effort to move away from the current achievement culture and toward a way of teaching math that builds conceptual understanding, my team and I decided to embark on an ambitious math project: to build a scale model of a million.
Multiplying Decimals. In Texas, multiplying decimals with products to the hundredths was added to the 5th grade curriculum last year, and today I tackled it with some of our 5th graders.

Shifting from multiplying whole numbers to multiplying decimals is a huge shift, so that means that the learning needs to be concrete. Time to bring out the base-10 blocks. As I was planning for my lesson, I thought through all the variations related to multiplying with decimals, and here’s what I came up with:Whole number factor times mixed number factor (eg., 2 x 1.3)Mixed number factor times mixed number factor (eg., 1.3 x 1.5)Whole number factor times a decimal factor (eg., 2 x 0.8)Mixed number factor times a decimal factor (eg., 1.3 x 0.4)Decimal factor times a decimal factor (eg., 0.7 x 0.3)
Flexibility with Place Value. New standards call for an increased emphasis on understanding place value, rather than just, for example, identifying the digit in a certain place value position (eg., In the number 345, what digit is in the hundreds place?).
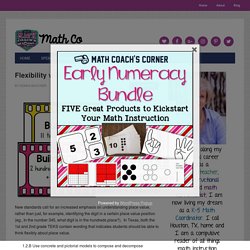
In Texas, both the 1st and 2nd grade TEKS contain wording that indicates students should be able to think flexibly about place value. Do You Have the Power of Ten.pdf. 5th Grade: Decimal Place Value – Illustrative Mathematics. The Difference Between Knowing and Understanding Place Value. My 2nd graders have been exploring place value, so yesterday I wrote the number 43 on the table in front of one sweet friend and asked what he could tell me about the number 43. He proudly told me it was 4 tens and 3 ones. This is very common, right? We ask students to name the place value positions or tell us what digit is in the tens place, etc.
I handed him a student ten-frame kit and asked him to build the number 43 using ten-frames. He immediately reached for a 4 tile. The Difference Between Knowing and Understanding Place Value. Place Value-Building Meaning Behind the Numbers. Hi Donna, I am from Melbourne, Australia and am a keen follower of your blog! In 2014 I completed my PhD in whole number place value. I, like you, believe that our students need a much deeper understanding of place value than many currently have. My research showed that there are students whom I described as “apparent experts”. They appear to understand place value, i.e: they can identify the value of the columns, read, write and order numbers, but when we ask them to rename numbers or compose or decompose numbers in a non-standard way they flounder. Multiplying Decimals. Extending Multiplication to Larger Numbers. The transition from additive thinking to multiplicative thinking is very difficult and abstract for some kiddos.
Think about it, for as long as they’ve been working with numbers, the number 2 has represented two things. Two ducks, two cookies, two linking cubes, etc. Now, with multiplication, 2 x 8 means 2 groups of 8. That’s huge. So, of course, it’s important that students get LOTS of concrete practice with the concept of multiplication–building 2 groups of 8. I Love Number Lines! Flexibility with Place Value. 5th Grade: Decimal Place Value.