

Zenzizenzizenzic. Zenzizenzizenzic is an obsolete form of mathematical notation representing the eighth power of a number (that is, the zenzizenzizenzic of a number x is the power x8), dating from a time when powers were written out in words rather than as superscript numbers.
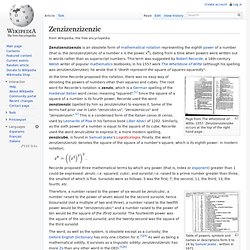
This term was suggested by Robert Recorde, a 16th-century Welsh writer of popular mathematics textbooks, in his 1557 work The Whetstone of Witte (although his spelling was zenzizenzizenzike); he wrote that it "doeth represent the square of squares squaredly". Page from The Whetstone of Witte, 1557. Zenzizenzizenzike occurs at the top of the right hand page. At the time Recorde proposed this notation, there was no easy way of denoting the powers of numbers other than squares and cubes.
Recorde proposed three mathematical terms by which any power (that is, index or exponent) greater than 1 could be expressed: zenzic, i.e. squared; cubic; and sursolid, i.e. raised to a prime number greater than three, the smallest of which is five. Yuktibhāṣā. Contents[edit] Mathematics[edit] As per the old Indian tradition of starting off new chapters with elementary content, the first four chapters of the Yuktibhasa contain elementary mathematics, such as division, proof of Pythagorean theorem, square root determination, etc.[8] The radical ideas are not discussed until the sixth chapter on circumference of a circle.
List of paradoxes. This is a list of paradoxes, grouped thematically.
The grouping is approximate, as paradoxes may fit into more than one category. Because of varying definitions of the term paradox, some of the following are not considered to be paradoxes by everyone. This list collects only scenarios that have been called a paradox by at least one source and have their own article. Although considered paradoxes, some of these are based on fallacious reasoning, or incomplete/faulty analysis. Informally, the term is often used to describe a counter-intuitive result. Logic[edit] Self-reference[edit] Squircle. There are two incompatible definitions of the squircle.
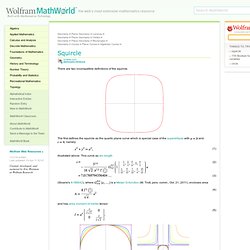
The first defines the squircle as the quartic plane curve which is special case of the superellipse with and , namely illustrated above. This curve as arc length (Sloane's A186642), where is a Meijer G-function (M. And has area moment of inertia tensor The second definition of the squircle was given by Fernandez Guasti (1992), but apparently not dubbed with the name "squircle" until later (Fernández Guasti et al. 2005).
With squareness parameter , where corresponds to a circle with radius to a square of side length . To exclude other branches. Where. Ishango bone. The Ishango bone is a bone tool, dated to the Upper Paleolithic era.
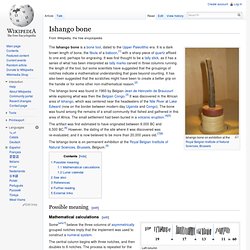
It is a dark brown length of bone, the fibula of a baboon,[1] with a sharp piece of quartz affixed to one end, perhaps for engraving. It was first thought to be a tally stick, as it has a series of what has been interpreted as tally marks carved in three columns running the length of the tool, but some scientists have suggested that the groupings of notches indicate a mathematical understanding that goes beyond counting. It has also been suggested that the scratches might have been to create a better grip on the handle or for some other non-mathematical reason.[2] The Ishango bone was found in 1960 by Belgian Jean de Heinzelin de Braucourt while exploring what was then the Belgian Congo.[3] It was discovered in the African area of Ishango, which was centered near the headwaters of the Nile River at Lake Edward (now on the border between modern-day Uganda and Congo). Possible meaning[edit] Mathematical calculations[edit]
Ethnomathematics. In mathematics education, ethnomathematics is the study of the relationship between mathematics and culture.[1] Often associated with "cultures without written expression",[2] it may also be defined as "the mathematics which is practised among identifiable cultural groups".[3] It refers to a broad cluster of ideas ranging from distinct numerical and mathematical systems to multicultural mathematics education.
Erdős–Straus conjecture. Brahmagupta–Fibonacci identity. For example, The identity is a special case (n = 2) of Lagrange's identity, and is first found in Diophantus.
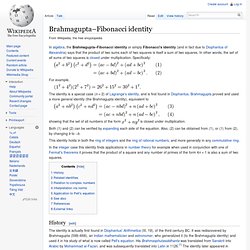
Brahmagupta proved and used a more general identity (the Brahmagupta identity), equivalent to showing that the set of all numbers of the form is closed under multiplication. Both (1) and (2) can be verified by expanding each side of the equation. This identity holds in both the ring of integers and the ring of rational numbers, and more generally in any commutative ring. Āryabhaṭīya. Āryabhaṭīya or Āryabhaṭīyaṃ, a Sanskrit astronomical treatise, is the magnum opus and only surviving work of the 5th century Indian mathematician, Āryabhaṭa.
Structure and style[edit] The text is written in Sanskrit and divided into four sections, covering a total of 121 verses that describe different results using a mnemonic style typical for such works in India. 1. Gitikapada: (13 verses): large units of time—kalpa, manvantra, and yuga—which present a cosmology different from earlier texts such as Lagadha's Vedanga Jyotisha(ca. 1st century BCE). There is also a table of sines (jya), given in a single verse. 2. 3. 4.