

Ejemplo de un Fractal. Dimensión fractal. La medición de formas fractales (fronteras, poligonales, etc,) ha obligado a introducir conceptos nuevos que van más allá de los conceptos geométricos clásicos.

Dado que un fractal está constituido por elementos cada vez más pequeños, el concepto de longitud no está claramente definido: Cuando se quiere medir una linea fractal con una unidad, o con un instrumento de medida determinado, siempre habrá objetos más finos que escaparán a la sensibilidad de la regla o el instrumento utilizado, y también a medida que aumenta la sensibilidad del instrumento aumenta la longitud de la línea. Esto sucede con la curva de Koch. Cada paso en la génesis de la curva aumenta un tercio su longitud. Es decir la longitud de la curva que ocupa el espacio inicial va aumentando en cada paso su longitud de forma indefinida.
Cada curva es 4/3 de la anterior: Así por ejemplo en el caso de la curva poligonal de nivel 10, la longitud es 1.(4/3)^(10-1): cualquiera que sea L: Cualquiera que sea L: D= log (N(L))/log(1/L) Complejidad. Por Inés Moisset Hasta el siglo pasado, la ciencia enseñaba que el cosmos se podía considerar como una máquina perfectamente predecible que se regía bajo la ley y el orden.

Este modelo idealizado se derrumbó y tras el equilibrio aparente surgió una nueva visión de la naturaleza que aprecia la complejidad de las relaciones. El orden perfecto de las formas de Euclides o Descartes no representa adecuadamente la geometría de la naturaleza. Las curvas regulares, como el círculo, son casos particularísimos. La realidad se revela tan irregular que el modelo continuo y perfectamente homogéneo fracasa y no puede servir ni siquiera como una primera aproximación. La discusión de estos nuevos conceptos surgió a fines del siglo XIX y principios del siglo XX, cuando matemáticos como Cantor, Von Koch y Peano comenzaron a dibujar curvas diferentes a las que se habían visto hasta entonces. ¿Cómo trasladar las ideas abstractas y los esquemas geométricos a la arquitectura? Notas: Me gusta: Dimensión Fraccionaria PDF. Autosimilaridad. Una curva de Koch presenta una autosimilaridad exacta infinitamente repitiente a medida que se aumenta su tamaño.
En Matemática, la autosimilaridad, a veces llamada autosimilitud o autosemejanza, es la propiedad de un objeto (llamado objeto autosimilar) en el que el todo es exacta o aproximadamente similar a una parte de sí mismo, por ejemplo cuando el todo tiene la misma forma que una o varias de sus partes. Muchos objetos del mundo real, como las costas marítimas, son estadísticamente autosimilares: partes de ella muestran las mismas propiedades estadísticas en diversas escalas.[1] La autosimilaridad es una propiedad de los fractales. Tipos de autosimilaridad[editar] El término autosimilaridad se usa informalmente para diferentes conceptos desde el punto de vista matemática. Informalmente, todas las formas de autosimilaridad entrañan un parecido estructural entre un objeto geométrico y una parte del mismo, es decir, existe parecido a diferentes escalas.
Autosimilaridad exacta[editar] Video de Autosimilitud. Perímetro Infinito. ¿De dónde salen las dimensiones fraccionarias o fractales?

La pregunta del título de este trabajo me llevó a averiguar en Internet y a encontrar varias definiciones del concepto de dimensión, de las cuales las dimensión euclídea es la menos general. Sin embargo ésta siempre coincide con las definiciones más generales en los casos que ella abarca. Y la definición de Hausdorff-Besicovitch que es en la que entran los fractales, no es una excepción. La definición es la siguiente: “Pick a point in a metric space. “How many disks does it take to cover the Koch coastline? Where N(h) is the number of disks of size h needed to cover the object. [Tomado de la página de Glen Elert, The Chaos HyperTextbook, About Dimension (3.3. Y ahora, ¿dónde estaba el error el razonamiento? [Tomado de la página de Charles Vasallo, Notion de dimension fractale.] Nótese que en el último caso (ángulo de 90 grados), como en la curva de Peano, la dimensión es entera. Paradógico copo de Nieve.
Conjunto de Mandelbrot. Representación matemática del conjunto de Mandelbrot como subconjunto del plano complejo.
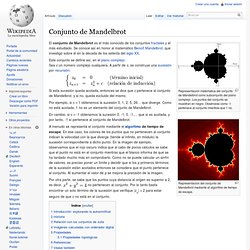
Los puntos del conjunto se muestran en negro. Obsérvese cómo -1 pertenece al conjunto mientras que 1 no. Representación del conjunto de Mandelbrot mediante el algoritmo de tiempo de escape. El conjunto de Mandelbrot es el más conocido de los conjuntos fractales y el más estudiado. Se conoce así en honor al matemático Benoît Mandelbrot, que investigó sobre él en la década de los setenta del siglo XX. Este conjunto se define así, en el plano complejo: Sea c un número complejo cualquiera. Si esta sucesión queda acotada, entonces se dice que c pertenece al conjunto de Mandelbrot, y si no, queda excluido del mismo. Por ejemplo, si c = 1 obtenemos la sucesión 0, 1, 2, 5, 26… que diverge.
En cambio, si c = -1 obtenemos la sucesión 0, -1, 0, -1,… que sí es acotada, y por tanto, -1 sí pertenece al conjunto de Mandelbrot. A menudo se representa el conjunto mediante el algoritmo de tiempo de escape.