

TEST DE NORMALITÉ. TEST DU KHI-DEUX. Statistiques. statophobes. 1 1 Statistiques pour statophobes Une introduction au monde des tests statistiques à l'intention des étudiants qui n'y entravent que pouic et qui détestent les maths par dessus le marché Denis Poinsot 2004 La libre reproduction et la diffusion de ce document sont non seulement autorisées mais les bienvenues du moment qu'elles sont réalisées dans un but pédagogique et non lucratif.
Pour citer ce document : D. Poinsot, Statistiques pour statophobes. [en ligne : 2 2 Ce petit livre est dédié avec reconnaissance à René Merckhoffer, mon extraordinaire prof de maths de classe de seconde au lycée des sept mares d'elancourt en 1982, pour son humour pince sans rire, mais surtout pour avoir réussi à m'arracher même très momentanément du fond de l'abîme mathématique dans lequel j'avais sombré sans espoir de revoir la lumière du jour. S'il n'avait pas été là au bon moment je n'aurais tout simplement pas pu faire d'études scientifiques. 3 3 Avant Propos Je suis biologiste, et non statisticien.
Cours de maths en PDF - exercices corrigés gratuits - sujets du brevet et bac S – POURQUOI avoir créé les NOMBRES COMPLEXES et pourquoi i ne peut s'écrire √ -1. Table of Contents - Math Open Reference.
Strophoïde. Construction de la strophoïde droite de pôle X et de point fixe O, en prenant pour courbe de base l'axe Oy.
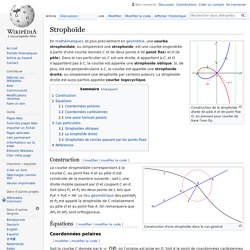
En mathématiques, et plus précisément en géométrie, une courbe strophoïdale, ou simplement une strophoïde, est une courbe engendrée à partir d'une courbe donnée C et de deux points A (le point fixe) et O (le pôle). Dans le cas particulier où C est une droite, A appartient à C, et O n'appartient pas à C, la courbe est appelée une strophoïde oblique. Si, de plus, OA est perpendiculaire à C, la courbe est appelée une strophoïde droite, ou simplement une strophoïde par certains auteurs. La strophoïde droite est aussi parfois appelée courbe logocyclique. Construction[modifier | modifier le code] Construction d'une strophoïde dans le cas général La courbe strophoïdale correspondant à la courbe C, au point fixe A et au pôle O est construite de la manière suivante : soit L une droite mobile passant par O et coupant C en K.
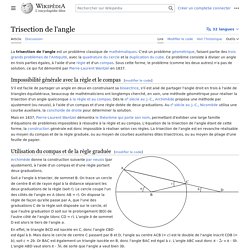
Équations[modifier | modifier le code] Soit la courbe C donnée par. Les tables de multiplication. LeMemento.fr : memento et formulaire technique. Trisection de l'angle. Impossibilité générale avec la règle et le compas[modifier | modifier le code] Mais en 1837, Pierre-Laurent Wantzel démontra le théorème qui porte son nom, permettant d'exhiber une large famille d'équations de problèmes impossibles à résoudre à la règle et au compas.
Sans titre. Table de logarithmes. Un article de Wikipédia, l'encyclopédie libre.
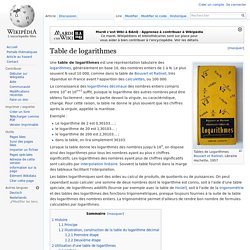
Une table de logarithmes est une représentation tabulaire des logarithmes, généralement en base 10, des nombres entiers de 1 à N. Le plus souvent N vaut 10 000, comme dans la table de Bouvart et Ratinet, très répandue en France avant l'apparition des calculettes, ou 100 000. La connaissance des logarithmes décimaux des nombres entiers compris entre 10n et 10n+1 suffit, puisque le logarithme des autres nombres peut être obtenu facilement ; seule la partie devant la virgule, ou caractéristique, change. Pour cette raison, la table ne donne le plus souvent que les chiffres après la virgule, appelée la mantisse. Exemple : Le logarithme de 2 est 0,30103… ;le logarithme de 20 est 1,30103… ;le logarithme de 200 est 2,30103… ;dans la table, on lira simplement 30103.
Lorsque la table donne les logarithmes des nombres jusqu'à 10n, on dispose ainsi des logarithmes pour tous les nombres ayant au plus n chiffres significatifs. Log(1,53) Liste des nombres premiers jusqu'a 1000000000000. Ruban de Pascal. Un article de Wikipédia, l'encyclopédie libre.
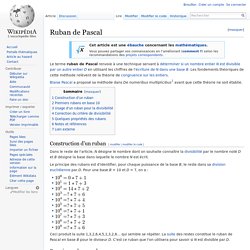
Résidu d'un entier naturel. Un article de Wikipédia, l'encyclopédie libre.
Pour les articles homonymes, voir résidu. Liste de critères de divisibilité. Un article de Wikipédia, l'encyclopédie libre.
Ceci est une liste de critères de divisibilité des nombres écrits en base décimale, exposés sans démonstration. Pour les démonstrations ou les méthodes ayant permis d'établir ces critères, voir l'article Critère de divisibilité. Dans tout cet article, un nombre de n chiffres est représenté par étant le chiffre des unités. étant le chiffre des dizaines. étant le chiffre des centaines. Test de primalité Miller-Rabin - cryptosec.
Test de primalité Miller-Rabin A la recherche de nombres premiers...

Généralités : Les algorithmes comme RSA ou Diffie-Hellman ont besoin de nombres premiers pour fonctionner.Pour générer ces nombres premiers on fait appel à des tests probabilistes. Les nombres ainsi trouvés sont premiers avec une certaine probabilité (très grande) paramétrable lors des implémentations.Factoriser un grand nombre, ou essayer de le faire, est très long. CATEGORIE DE NOMBRES : Maths-rometus, Nombres entiers, Nombres décimaux, Nombres rationnels, Nombres irrationnels, Nombres réels, Nombres complexes, Mathématiques, Maths, Math, Jean-Luc Romet. 1) Introduction : Les ensembles de nombres sont "gigognes", comme les poupées, on peut classer les nombres entiers naturels dans les nombres entiers relatifs qui sont eux-mêmes des nombres décimaux.
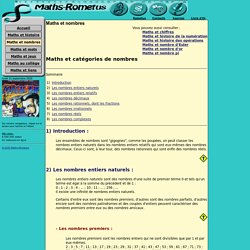
Ceux-ci sont, à leur tour, des nombres rationnels qui sont enfin des nombres réels. 2) Les nombres entiers naturels : Algorithme de calcul de la racine n-ième. Un article de Wikipédia, l'encyclopédie libre.
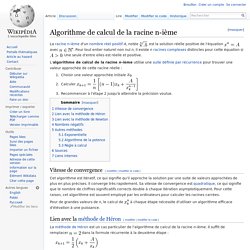
La racine n-ième d'un nombre réel positif A, notée , est la solution réelle positive de l'équation. Méthode de Héron. Un article de Wikipédia, l'encyclopédie libre. En mathématiques, la méthode de Héron ou méthode babylonienne est une méthode efficace d'extraction de racine carrée. Elle porte le nom du mathématicien Héron d'Alexandrie mais certains calculs antérieurs semblent prouver que la méthode est plus ancienne. Principe[modifier | modifier le code] Comment calculer une racine carrée à la main. 2 méthodes:En utilisant la décomposition en facteursComment trouver une racine carrée à la main Avant que n'arrivent les calculatrices et autres ordinateurs, on était bien obligé de calculer les racines carrées à la main, c'est ce que faisaient les étudiants et leurs professeurs. Il existe différentes méthodes pour calculer la racine carrée d'un nombre à la main.
Alors que certaines méthodes ne vous donneront qu'un résultat approché, d'autres permettent d'obtenir une précision remarquable. Extraction d'une racine carrée comme autrefois. Il existe de nombreux algorithmes pour calculer la racine carrée d'un nombre positif. Ma page sur le gnomon montre comment la trouver à une unité près, avec de simples soustractions de nombres impairs consécutifs. Il y a aussi une méthode géométrique utilisant la règle et le compas. L'algorithme de Héron d'Alexandrie Chez les mathématiciens grecs, extraire la racine carrée de a revient à trouver un carré dont l'aire est a : on cherche un carré qui a la même aire qu'un rectangle donné (origine agricole). En prenant un rectangle de côté arbitraire x et de même aire a, il est nécessaire que l'autre côté ait pour longueur a/x. Pour le rendre « moins rectangle », il suffit de considérer un nouveau rectangle dont la longueur est la moyenne arithmétique des deux côtés précédents soit et dont l'aire reste a.
Factorisation, test de primalité de grand nombre. Le test de primalité (savoir si un nombre est un nombre premier) de cette page est adapté au nombre composé de plusieurs dixaines de chiffres. La décomposition en facteurs premiers peut être très longue, voir impossible même pour nos ordinateurs modernes et encore davantage pour un outil de calcul en ligne d'un site web. Nous avons limité l'entrée au nombre composé au maximum de 200 chiffres pour le test et de 22 chiffres pour la factorisation en en facteurs premiers. Vous pouvez obtenir par exemples lesa décomposition :
FractInt Distribution. There are many ways to get the FractInt program. The easiest way for you may be right here. Click on the high-lighted text or button to retrieve the latest DOS version of FractInt. The latest release is FractInt version 20.4. Programmation des fractales. Commentaires Même avec le logiciel didactique Scratch, on obtient de bons résultats. Démarrage en cliquant sur le drapeau vert. Effacer tout sur l'écran. Boucles en Y et en X avec iterY et iterX. Images des mathématiques.
Conversion d'Unités En Ligne - Utilisez Nos Outils de Conversion. Explorez les sciences du numérique - Accueil.