

Lelivrescolaire.fr : Sujets Grand Oral Maths PC SVT HGGSP NSI, avec préparation à la présentation et aux questions. 200 SUJETS DE GRAND ORAL. Préparation au grand oral - étude d’une trajectoire avec les outils mathématiques. Se préparer au Grand oral. 5 minutes ► Le jour de l’épreuve, vous proposez au jury deux questions que vous aurez préparées seul ou en groupe, avec l’aide de vos professeurs.
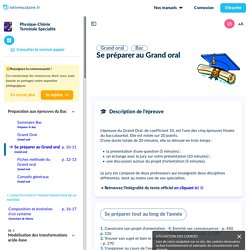
Ces deux questions portent sur les deux enseignements de spécialité conservés en terminale. Il peut s’agir de questions transversales, faisant appel aux deux spécialités ou de questions portant sur chacune des spécialités, prises séparément. ► Parmi ces deux questions, le jury en choisit une. S’ensuivent 20 minutes de préparation durant lesquelles il est possible de réaliser un support facultatif à l’attention du jury (schéma, carte mentale, graphique, etc.). 2020 12 14 Formation GO en PC. Physique et simulation. Accueil du site de Daniel Mentrard. Amphis pour Tous : Les mathématiques de l'arc en ciel. Scientia Egregia. Physique Appliquée. Des calculatrices pour presque tout ! Coding Games and Programming Challenges to Code Better.
Simulez des systèmes physiques avec la méthode d'Euler. En sciences, de nombreux phénomènes sont décrits par des équations différentielles dont la résolution exacte est parfois impossible ou peu intéressante.
On laisse alors de côté les méthodes analytiques pour travailler directement avec des nombres, en utilisant ce qu’on appelle des méthodes numériques de résolution d’équations différentielles. Ces méthodes permettent notamment de simuler des systèmes physiques, ce qui en fait un outil puissant pour les sciences et l’ingénierie. Ce tutoriel est une initiation à la simulation numérique, à travers la méthode la plus élémentaire qui soit : la méthode d’Euler explicite. Il est destiné aux gens ayant déjà été initiés aux équations différentielles de manière formelle et souhaitant découvrir comment les résoudre autrement. Méthode et démarche scientifiques. Pv140 Des chocs à pi : chocs et rebonds pv140. MATHÉMATIQUES ET RÉALITÉ par Pierre Cartier. Interdisciplinarité par Daniel Perrin: à consulter!!! Wandida, EPFL.
SI GALILÉE AVAIT ÉTÉ UN DATA SCIENTIST... L’image ci-dessus montre un échantillon extrait de notre ensemble de données : chaque ligne correspond à un lâcher de bille bien précis et consigne les mesures correspondantes.

Dans la suite, on notera la hauteur de chute (height), le temps de chute libre (fallTime) et la vitesse en fin de chute (speed) [1]. Face à un tel déluge de chiffres, il n’est pas facile d’extraire immédiatement une information pertinente. Un ordinateur quant à lui peut immédiatement calculer des moyennes, des corrélations, des indices, etc. Mesures à l'ancienne. Emilie du chatelet. MESURER UN ANGLE AVEC UNE BALANCE. Rediffusion d’un article publié le 4 octobre 2018 Une version mécaniste du théorème de Pythagore Piste rouge Le 26 mars 2021 - Ecrit par Aurélien Alvarez Dans les trousses des écoliers, on trouve bien souvent des crayons, une règle, un compas mais aussi un rapporteur.

Ce petit instrument, facile à utiliser, est très pratique pour mesurer des angles. POIDS, POULIES ET POINT DE FERMAT-STEINER. Le montage expérimental illustré sur la photo ci-dessus est très simple : trois masses égales sont reliées entre elles par des fils, et chacune des masses est suspendue à une poulie [1].

Lorsqu’on lâche les trois masses, après quelques secondes, une position d’équilibre est trouvée [2]. Si l’on regarde attentivement, on remarque que les trois angles autour du point de rencontre des trois fils sont égaux, donc mesurent chacun 120 degrés. Plutôt que d’utiliser un rapporteur pour vérifier cela, on peut construire et utiliser un petit gabarit en papier comme nous l’avions déjà proposé dans notre article précédent déjà mentionné. Math.ing : les Vecteurs et Galilée. Math.ing : les Vecteurs et Newton - WebTV Université de Lille.
E-Learning Physique. UN PLANIMÈTRE À CÔNE. Parmi les machines mathématiques qui furent exposées, on trouve ce magnifique planimètre à cône, remontant au dix-neuvième siècle.
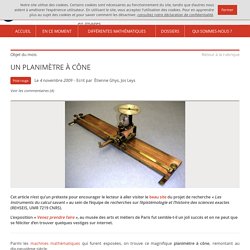
Il permet de mesurer l’aire sous une courbe, comme nous allons l’expliquer ici. Bien sûr, on n’en trouve plus dans les bureaux d’étude d’aujourd’hui ! D’autres planimètres bien plus efficaces ont été inventés par la suite et à l’avenir nous ne résisterons probablement pas au plaisir d’en décrire d’autres pour Images des Maths. Mais son fonctionnement, si simple et si astucieux, permet une meilleure compréhension des concepts d’aire et d’intégrale.
Mathématiques, Sciences physique chimie bac, annales, cours - Transition vers le supérieur. Equations Differentielles. Informatique appliqué aux Sciences Physiques. Enseignements - Yannick Privat. Enseignements Quelques documents pédagogiques Aspects théoriques et numériques pour les fluides incompressibles (master 2, mathématiques de la modélisation, UPMC, bac+5) Contrôle optimal (master 2, Calcul Scientifique et Mathématiques de l'Information, univ.

Strasbourg, bac+5) Optimisation (master 1, Strasbourg, bac+4) Optimisation non-linéaire (L3, Math-Eco, univ. Modélisation par suites et fonctions (Daniel Perrin) Méthodes scientifiques : angle et dimension. Coordonnées cartésiennes, cylindriques, sphériques...
Cours de Mathématiques pour la physique. Magie des Automates. Physagreg : Cours gratuits de physique chimie tous niveaux : collège, lycée, licence, capes et agrégation. Représentation mathématique de notions physiques. Analyse vectorielle. Des lois de Kepler au chaos. Mécanique des fluides. Maths Meteo APMEP Nodet. Prévisions météorologiques. Prévoir le temps est particulièrement difficile lorsque la circulation atmosphérique est instable.
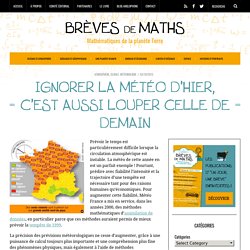
La météo de cette année en est un parfait exemple ! Pourtant, prédire avec fiabilité l’intensité et la trajectoire d’une tempête est nécessaire tant pour des raisons humaines qu’économiques. Pour augmenter cette fiabilité, Météo France a mis en service, dans les années 2000, des méthodes mathématiques d’assimilation de données, en particulier parce que ces méthodes auraient permis de mieux prévoir la tempête de 1999. De la météo au climat. Les changements à l’échelle du globe sont sans équivoque : hausse généralisée des températures de l’air et de la surface des océans, fonte accélérée de la neige et de la glace, élévation du niveau moyen de la mer.

Les émissions de gaz à effet de serre par les activités humaines causeront un réchauffement mondial durant le XXIe siècle qui excèdera fort probablement le réchauffement observé durant le XXe siècle]. Le premier énoncé provient de mesures prises sur un ensemble de variables climatologiques, échelonnées sur plusieurs décennies et dans plusieurs régions du globe. Energies renouvelables et Climat.
Mathématiques et turbulences (Robert) ANALYSE DES IMAGERIES DES INSTRUMENTS SCIENTIFIQUES DE L’ÉPOQUE MODERNE (XVIE-XVIIE SIÈCLE) Les multiples fonctions des instruments scientifiques à l’époque moderne A l’Observatoire de Paris se trouve un instrument scientifique du XVIe siècle, dont les riches illustrations présentent une véritable énigme pour le spectateur moderne.
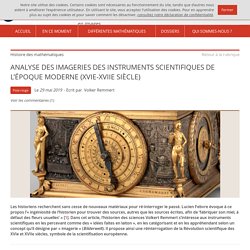
Ce cadran solaire, réalisé en 1578 par Wentzel Jamnitzer (c. 1507–1585), peut être considéré comme un objet de collection représentatif d’une époque révolue, dans laquelle légendes bibliques et mythes grecs étaient omniprésents. Alors que nos pensées se détournent déjà de cet objet, nous pouvons aussi nous étonner : pourquoi un instrument scientifique est-il muni d’une si riche imagerie ? Au seuil de ce que l’on a appelé la révolution scientifique, au début d’une mathématisation systématique des mondes sociaux et physiques, ne devrions-nous pas plutôt avoir des instruments conçus de manière simple et sobre ?
Figure 1 : Cadran solaire de Wentzel Jamnitzer, Nuremberg, 1572/78. Barycentre = centre des masses. Biomeca - Centre de masse segmentaire. Roger Itterbeek Mécanique. Jean Doyen : Les nombres premiers et l'hypothèse de Riemann. Jean Doyen : Le palimpseste de la méthode d' Archimède.
Parabole carree :calcul d'aire d'Archimède (suites arithm et géo) Intégrité scientifique. Corrélation Causalité. Mécanique : la méthode d'Euler, explications et exemple. Traitement du signal, transformées de Fourier. Richard Feynman. Quelques physiciens! Math Park - 25/03/2017 - Kirone MALLICK, ENTROPIE ET PHYSIQUE STATISTIQUE.
Physique statistique. La physique statistique a pour but d'expliquer le comportement et l'évolution de systèmes physiques comportant un grand nombre de particules (on parle de systèmes macroscopiques), à partir des caractéristiques de leurs constituants microscopiques (les particules). Ces constituants peuvent être des atomes, des molécules, des ions, des électrons, des photons, des neutrinos, ou des particules élémentaires. Ces constituants et les interactions qu'ils peuvent avoir entre eux sont en général décrits par la mécanique quantique, mais la description macroscopique d'un ensemble de tels constituants ne fait, elle, pas directement appel (ou en tout cas pas toujours) à la mécanique quantique.
De fait, cette description macroscopique, en particulier la thermodynamique, a été obtenue pour partie avant le développement de la mécanique quantique en tant que théorie de la physique, essentiellement dans la seconde moitié du XIXe siècle. Historique[modifier | modifier le code] sont égaux. POURQUOI LA MOUSSE LIQUIDE EST-ELLE SI SOLIDE ? Mettez un peu d’eau dans une bouteille, ajoutez quelques gouttes de liquide vaisselle, agitez : la mousse se forme. Avez-vous déjà essayé de la rincer ? Ne connaissez-vous rien de plus agaçant ? Cette écume, apparemment fugace et molle, résiste obstinément à toute tentative de la faire s’écouler à travers le goulot. Exposition «Maths & mesure» - Mesurer le monde. Math & Phys. TD de physique statistique, Master 1 de physique, UGA. 1 (TD) Travaux Dirigés 2 Anciens examens Examen CC 11 mars 2020. Température de fusion, Taux de ionisation d'un plasma. 3 Cours et livres Obtenir des livres de physique statistique en écrivant /documents à la place de /TD dans l'URL de cette page.Ou tous les livres scientifiques sur le site suivant, documents et livres, écrire le titre ou nom de l'auteur.Très recommandé: lire l'introduction de ce livre téléchargeable: Livre: « Statistical Mechanics of Lattice Systems: a Concrete Mathematical Introduction » de Sacha Friedli and Yvan VelenikNotes de cours de Arnaud Ralko (2019-2020).Notes de cours de Léonie Canet (2015-2016).
Expériences EPFL.
Science Calculators. Les idées froides. Tribologie. Les premières études empiriques sur les forces de friction sont attribuées à Léonard de Vinci[1]. La tribologie (du grec ancien τρίβος, « frottement » et λόγος, « science, étude ») est la science qui étudie les phénomènes susceptibles de se produire entre deux systèmes matériels en contact, immobiles ou animés de mouvements relatifs. Ce terme recouvre, entre autres, tous les domaines du frottement, de l’usure, de l'étude des interfaces et de la lubrification[2]. Liaisons mécaniques avec frottement.
Trop souvent considéré comme un élément perturbateur pour les calculs, on s’aperçoit très vite que le frottement est tout simplement indispensable : si les vis de fixation restent serrées, le clou en place, les échelles debout et les voitures sur la route, c’est grâce au frottement. C’est aussi sur ce phénomène que repose le fonctionnement des freins et embrayages.
Pour résoudre un problème de statique, sa considération systématique n’est pas obligatoire. Il existe des modèles mathématiques simples, et cependant précis qui décrivent ce phénomène. Les lois de Coulomb font partie de ces modèles. La tribologie est la science du contact qui propose d'autres modèles plus pointus à utiliser suivant les exigences de l'étude. PEUT-ON COMPRENDRE D’OÙ VIENT L'EFFICACITÉ DES MATHÉMATIQUES EN PHYSIQUE ? Modèles en jouet - Tadashi Tokieda. Your Smartphone Can Do Physics. Dans une conversation entre Alain Connes et Jacques Dixmier. La conduction, un moteur universel. Résistance des matériaux. Vagues, tourbillons, tsunamis. Les aqueducs romains (ambitieux) Châteaux d'eau.
Ligne d'écoulement. Liberté asymptotique. Vers l'infini et au delà : une histoire de distances cosmiques. Attraction ou distraction ? La représentation du mouvement par l image. ILS ONT DOMPTÉ LE HASARD #CMH3. La théorie des probabilités de Pascal à Kolmogorov (Benoît Rittaud) Les probabilités ont la cote ! [Conférence SML] Labyrinthes aléatoires et transition de phase - Sébastien Martineau. Math Park - 20/01/2018 - Nicolas CURIEN - MARCHES ALÉATOIRES ET RÉSEAUX ÉLÉCTRIQUES. Marches aléatoires.
Mouvements browniens et mouvements de foules. Modèles et calculs combinatoires - Interstices.