

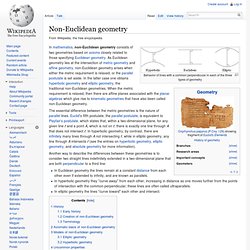
Non-Euclidean geometry. Behavior of lines with a common perpendicular in each of the three types of geometry In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those specifying Euclidean geometry.
As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises when either the metric requirement is relaxed, or the parallel postulate is set aside. In the latter case one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras which give rise to kinematic geometries that have also been called non-Euclidean geometry.
Another way to describe the differences between these geometries is to consider two straight lines indefinitely extended in a two-dimensional plane that are both perpendicular to a third line: History[edit] Early history[edit] Terminology[edit] Euclidean geometry. Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements.
Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians,[1] Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system.[2] The Elements begins with plane geometry, still taught in secondary school as the first axiomatic system and the first examples of formal proof. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, explained in geometrical language.[3] For more than two thousand years, the adjective "Euclidean" was unnecessary because no other sort of geometry had been conceived.
The Elements[edit] Axioms[edit] . Differential geometry. Symplectic geometry. Symplectic geometry is a branch of differential geometry and differential topology that studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form.
Symplectic geometry has its origins in the Hamiltonian formulation of classical mechanics where the phase space of certain classical systems takes on the structure of a symplectic manifold. Every Kähler manifold is also a symplectic manifold. Well into the 1970s, symplectic experts were unsure whether any compact non-Kähler symplectic manifolds existed, but since then many examples have been constructed (the first was due to William Thurston); in particular, Robert Gompf has shown that every finitely presented group occurs as the fundamental group of some symplectic 4-manifold, in marked contrast with the Kähler case. Name[edit] Symplectic geometry is also called symplectic topology although the latter is really a subfield concerned with important global questions in symplectic geometry. Riemannian geometry. Elliptic geometry is also sometimes called "Riemannian geometry".

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length of curves, surface area, and volume. From those some other global quantities can be derived by integrating local contributions. Riemannian geometry originated with the vision of Bernhard Riemann expressed in his inaugurational lecture Ueber die Hypothesen, welche der Geometrie zu Grunde liegen (On the Hypotheses which lie at the Bases of Geometry). It is a very broad and abstract generalization of the differential geometry of surfaces in R3. Introduction[edit] Riemannian geometry was first put forward in generality by Bernhard Riemann in the nineteenth century. The following articles provide some useful introductory material:
Information Geometry.