

How to split a cab fare fairly using game theory. I came across a fantastic game theory article that appeared in the Wall Street Journal Number’s Guy blog all the way back in 2005.
The article is about three friends who agree to share a cab, and the possible ways they can split the costs. I highly recommend you read the article. The thing I liked most is the article describes various fair division methods. As I have described before in my article about splitting restarant bills, fair division is not just a mathematical concept. Fair division depends on social norms and how people perceive fairness. Therefore, it is useful to understand many methods of fair division and have them in your toolkit.
The details of the cab ride The situation is a common one: three friends agree to share a cab to different destinations, and they need to split the costs fairly. More specifically, let us consider the following situation: Let’s say that passenger A’s usual fare would be $1, passenger B’s is $5 and passenger C’s is $9. Method 3: Bargaining solutions. Game theory. Game theory is the study of strategic decision making.
Specifically, it is "the study of mathematical models of conflict and cooperation between intelligent rational decision-makers. "[1] An alternative term suggested "as a more descriptive name for the discipline" is interactive decision theory.[2] Game theory is mainly used in economics, political science, and psychology, as well as logic, computer science, and biology. The subject first addressed zero-sum games, such that one person's gains exactly equal net losses of the other participant or participants. Today, however, game theory applies to a wide range of behavioral relations, and has developed into an umbrella term for the logical side of decision science, including both humans and non-humans (e.g. computers, animals).
Strategy (game theory) The strategy concept is sometimes (wrongly) confused with that of a move.
A move is an action taken by a player at some point during the play of a game (e.g., in chess, moving white's Bishop a2 to b3). A strategy on the other hand is a complete algorithm for playing the game, telling a player what to do for every possible situation throughout the game. A strategy profile (sometimes called a strategy combination) is a set of strategies for all players which fully specifies all actions in a game. A strategy profile must include one and only one strategy for every player. A player's strategy set defines what strategies are available for them to play.
Best response. Best response correspondence[edit] Figure 1.
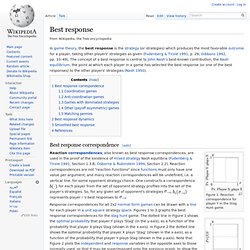
Reaction correspondence for player Y in the Stag Hunt game. , for each player from the set of opponent strategy profiles into the set of the player's strategies. So, for any given set of opponent's strategies represents player i 's best responses to. Strategic dominance. Terminology[edit] When a player tries to choose the "best" strategy among a multitude of options, that player may compare two strategies A and B to see which one is better.
The result of the comparison is one of: B dominates A: choosing B always gives as good as or a better outcome than choosing A. There are 2 possibilities: B strictly dominates A: choosing B always gives a better outcome than choosing A, no matter what the other player(s) do.B weakly dominates A: There is at least one set of opponents' action for which B is superior, and all other sets of opponents' actions give B the same payoff as A.B and A are intransitive: B neither dominates, nor is dominated by, A. Choosing A is better in some cases, while choosing B is better in other cases, depending on exactly how the opponent chooses to play. This notion can be generalized beyond the comparison of two strategies. Pareto efficiency. Pareto efficiency, or Pareto optimality, is a state of allocation of resources in which it is impossible to make any one individual better off without making at least one individual worse off.
The term is named after Vilfredo Pareto (1848–1923), an Italian economist who used the concept in his studies of economic efficiency and income distribution. [citation needed] The concept has applications in academic fields such as economics and engineering. For example, suppose there are two consumers A & B and only one resource X. Suppose X is equal to 20. Let us assume that the resource has to be distributed equally between A and B and thus can be distributed in the following way: (1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (7,7), (8,8), (9,9), (10,10).
Nash equilibrium. In game theory, the Nash equilibrium is a solution concept of a non-cooperative game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only their own strategy.[1] If each player has chosen a strategy and no player can benefit by changing strategies while the other players keep theirs unchanged, then the current set of strategy choices and the corresponding payoffs constitutes a Nash equilibrium.
The reality of the Nash equilibrium of a game can be tested using experimental economics method. Stated simply, Amy and Will are in Nash equilibrium if Amy is making the best decision she can, taking into account Will's decision while Will's decision remains unchanged, and Will is making the best decision he can, taking into account Amy's decision while Amy's decision remains unchanged. Applications[edit] History[edit] The Nash equilibrium was named after John Forbes Nash, Jr. Let . Perfect information. Perfect information is a situation in which an agent has all the relevant information with which to make a decision.
It has implications for several fields. Game theory[edit] In game theory, an extensive-form game has perfect information if each player, when making any decision, is perfectly informed of all the events that have previously occurred. [1] Card games where each player's cards are hidden from other players are examples of games with imperfect information.[2][3] Subgame perfect equilibrium. A subgame perfect equilibria necessarily satisfies the One-Shot deviation principle.
The set of subgame perfect equilibria for a given game is always a subset of the set of Nash equilibria for that game. In some cases the sets can be identical. Folk theorem (game theory) For an infinitely repeated game, any Nash equilibrium payoff must weakly dominate the minmax payoff profile of the constituent stage game.
This is because a player achieving less than his minmax payoff always has incentive to deviate by simply playing his minmax strategy at every history. The folk theorem is a partial converse of this: A payoff profile is said to be feasible if it lies in the convex hull of the set of possible payoff profiles of the stage game. The folk theorem states that any feasible payoff profile that strictly dominates the minmax profile can be realized as a Nash equilibrium payoff profile, with sufficiently large discount factor. For example, in the Prisoner's Dilemma, both players cooperating is not a Nash equilibrium. Grim trigger. In game theory, grim trigger (also called the grim strategy or just grim) is a trigger strategy for a repeated game, such as an iterated prisoner's dilemma.
Initially, a player using grim trigger will cooperate, but as soon as the opponent defects (thus satisfying the trigger condition), the player using grim trigger will defect for the remainder of the iterated game. Since a single defect by the opponent triggers defection forever, grim trigger is the most strictly unforgiving of strategies in an iterated game. In iterated prisoner's dilemma strategy competitions, grim trigger performs poorly even without noise, and adding signal errors makes it even worse. Its ability to threaten permanent defection gives it a theoretically effective way to sustain trust, but because of its unforgiving nature and the inability to communicate this threat in advance, it performs poorly.[1] See also[edit]
Repeated game. In game theory, a repeated game (supergame or iterated game) is an extensive form game which consists in some number of repetitions of some base game (called a stage game). The stage game is usually one of the well-studied 2-person games. It captures the idea that a player will have to take into account the impact of his current action on the future actions of other players; this is sometimes called his reputation.
Bayesian game. In game theory, a Bayesian game is one in which information about characteristics of the other players (i.e. payoffs) is incomplete. Following John C. Cooperative game. This article is about a part of game theory. For video gaming, see Cooperative gameplay. For the similar feature in some board games, see cooperative board game In game theory, a cooperative game is a game where groups of players ("coalitions") may enforce cooperative behaviour, hence the game is a competition between coalitions of players, rather than between individual players. Normal-form game. In static games of complete, perfect information, a normal-form representation of a game is a specification of players' strategy spaces and payoff functions.
A strategy space for a player is the set of all strategies available to that player, whereas a strategy is a complete plan of action for every stage of the game, regardless of whether that stage actually arises in play. A payoff function for a player is a mapping from the cross-product of players' strategy spaces to that player's set of payoffs (normally the set of real numbers, where the number represents a cardinal or ordinal utility—often cardinal in the normal-form representation) of a player, i.e. the payoff function of a player takes as its input a strategy profile (that is a specification of strategies for every player) and yields a representation of payoff as its output.
An example[edit] Other representations[edit] Uses of normal form[edit] Dominated strategies[edit] Sequential games in normal form[edit] such that. Extensive-form game. Minimax. Minimax (sometimes MinMax or MM[1]) is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case (maximum loss) scenario. Originally formulated for two-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision making in the presence of uncertainty.
Backward induction. Markov decision process. Markov decision processes (MDPs), named after Andrey Markov, provide a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via dynamic programming and reinforcement learning. MDPs were known at least as early as the 1950s (cf. Bellman 1957). Fictitious play. In game theory, fictitious play is a learning rule first introduced by G.W. Regret (decision theory) Regret (also called opportunity loss) is defined as the difference between the actual payoff and the payoff that would have been obtained if a different course of action had been chosen. This is also called difference regret. Prisoner's dilemma. Ultimatum game. Matching pennies.
Battle of the sexes. Coordination game.