

Pythagorean Theorem, Euclid's Proof VI.31. (VI.20) Similar polygons are divided into similar triangles, and into triangles equal in multitude and in the same ratio as the wholes, and the polygon has to the polygon a ratio duplicate of that which the corresponding side has to the corresponding side.
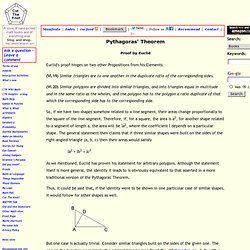
So, if we have two shapes somehow related to a line segment, their areas change proportionally to the square of the line segment. Therefore, if, for a square, the area is a2, for another shape related to a segment of length a, the area will be la2, where the coefficient l depends on a particular shape. The general statement then claims that if three similar shapes were built on the sides of the right-angled triangle then their areas would satisfy As we mentioned, Euclid has proven his statement for arbitrary polygons. Although the statement itself is more general, the identity it leads to is obviously equivalent to that asserted in a more traditional version of the Pythagoras' Theorem. The Pythagorean Theorem. Department of Mathematics Education J.

Wilson, EMT 669 The Pythagorean Theorem by Stephanie J. Pythagorean Triples. Pythagorean Triples By Kelly Edenfield The Pythagorean theorem is used in all aspects of mathematics.

However, the algebra assoicated with the generating of the triples that satisfy the theorem is often overlooked. Just as the nature of the theorem was known before Pythagoras' time, so was the idea of the triples. As early as 1900 to 1600 B. Pythagoras (c. 540 B.C.) presented a formula for generating triples. If we begin with a square figure representing n2, the dots placed around it will be 2n + 1, and the resulting square will be (n + 1)2. Since we are looking for triples of squared numbers, let 2n + 1 = m2. m2 + ((m2 - 1)/2)2 = ((m2 + 1)/2)2, where m must be odd. Plato (c. 380 B. A more general formula for obtaining all triples was given by Euclid (c. 300 B.C.) in his book Elements: (2uv)2 + (u2 - v2)2 = (u2 + v2)2, where u and v have no common factors, u > v, amd one of u and v is odd and the other is even.
Pythagorean Triples - Advanced. (You may like to read about Pythagoras' Theorem or an Introduction to Pythagorean Triples first) A "Pythagorean Triple" is a set of positive integers, a, b and c that fits the rule: a2 + b2 = c2.
Pythagorean Triple Information, Pythagorean Triple Reference Articles - FindTarget Reference. Pythagorean triple. Pythagorean triple. Pythagorean Triplets, Triples. "Pythagorean triples" are integer solutions to the Pythagorean Theorem, a2 + b2 = c2.

I like "triplets," but "triples" seems to be the favored term. The Pythagorean Theorem. Return to my Mathematics pages Go to my home page Note: If your WWW browser cannot display special symbols, like ² or 2 or ±, then click here for the alternative Pythagorean Theorem page. © Copyright 1997, Jim Loy. Pythagorean Triples. III.

Counting Triples Definition Two triples are siblings if they have a common hypotenuse. The first such pair of primitive triples stem from the hypotenuse 65 (332 + 562 = 632 + 162 = 652): There are also primitive siblings of the hypotenuse 85: If we search larger numbers, we can find larger sets of siblings. In general, the number of primitive Pythagorean triples of hypotenuse n is dependent on the number of prime factors of n that are congruent to 1 modulo 4.
The hypotenuse 32045 has eight primitive triples: But why do primitive triples form only in sets of 2α, and what is the connection to primes p ≡ 1 mod 4? By examining the data, it appears that the prime factors of each hypotenuse satisfy p ≡ 1 mod 4. Of course, explaining where 2ω(z) – 1 arises is more tricky. Theorem 3 (Fermat) Let p be a prime such that p ≡ 1 mod 4. By "uniquely" it is meant that there exist unique integers a and b such that 0 < a < b and p = a2 + b2. For example, for n = 1105, Proof. Pythagtriple.pdf (application/pdf-objek) The Thirty Greatest Mathematicians. Click for a discussion of certain omissions.

Please send me e-mail if you believe there's a major flaw in my rankings (or an error in any of the biographies). Obviously the relative ranks of, say Fibonacci and Ramanujan, will never satisfy everyone since the reasons for their "greatness" are different. I'm sure I've overlooked great mathematicians who obviously belong on this list. Please e-mail and tell me! Pythagorean Triangles and Triples. The calculators on this page require JavaScript but you appear to have switched JavaScript off (it is disabled).

Please go to the Preferences for this browser and enable it if you want to use the calculators, then Reload this page. Right-angled triangles with whole number sides have fascinated mathematicians and number enthusiasts since well before 300 BC when Pythagoras wrote about his famous "theorem". The oldest mathematical document in the world, a little slab of clay that would fit in your hand, is a list of such triangles. So what is so fascinating about them? This page starts from scratch and has lots of facts and figures with several online calculators to help with your own investigations. 1 Right-angled Triangles and Pythagoras' Theorem 1.1 Pythagoras and Pythagoras' Theorem Pythagoras was a mathematician born in Greece in about 570 BC. Pythagorean theorem. Pythagorean Triples. Three integers a, b, and c that satisfy a2 + b2 = c2 are called Pythagorean Triples.
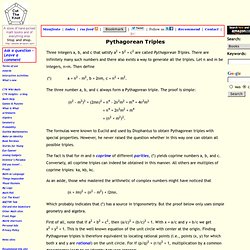
There are infinitely many such numbers and there also exists a way to generate all the triples. Let n and m be integers, n>m. Then define.