

Free Will. 1.
Rational Deliberation 1.1 Free Will as Choosing on the Basis of One's Desires On a minimalist account, free will is the ability to select a course of action as a means of fulfilling some desire. David Hume, for example, defines liberty as “a power of acting or of not acting, according to the determination of the will.” (1748, sect.viii, part 1). And we find in Jonathan Edwards (1754) a similar account of free willings as those which proceed from one's own desires. One reason to deem this insufficient is that it is consistent with the goal-directed behavior of some animals whom we do not suppose to be morally responsible agents. 1.2 Free Will as deliberative choosing on the basis of desires and values A natural suggestion, then, is to modify the minimalist thesis by taking account of (what may be) distinctively human capacities and self-conception. Free Will and Determinism. Articles Michael Norwitz examines the current state of play in this long-running debate, by comparing the views of Dennett and van Inwagen.
Since the ancient Greeks, one of the most provocative and oft-discussed questions in philosophy has been whether we have free will in determining the course of our actions, or whether our actions are determined by forces beyond our control. Before the advent of secular thought, those forces might have been identified as the whims of the gods, though the tradition of naturalism in Western thought goes back at least as far as the Milesian School of Greek Philosophy, in the 6th century B.C. In more recent times as the cognitive sciences have developed, it has seemed increasingly likely that our brains work along deterministic lines (or, if quantum effects are non-negligible, at the very least along mechanical lines).
For the third premise van Inwagen does not present a concise summary of his line of argument. . © Michael Norwitz 1991. Oxford Institute for Ethics, Law and Armed Conflict. DIY & Science Toys. Budget Bytes - My stomach is full and my wallet is too. Broke & Healthy. Mathematical induction - Topics in precalculus. The principle of mathematical induction THE NATURAL NUMBERS are the counting numbers: 1, 2, 3, 4, etc.

Mathematical induction is a technique for proving a statement -- a theorem, or a formula -- that is asserted about every natural number. By "every", or "all," natural numbers, we mean any one that we might possibly name. For example, 1 + 2 + 3 + . . . + n = ½n(n + 1). This asserts that the sum of consecutive numbers from 1 to n is given by the formula on the right. -- which is true. But how are we to prove this rule for every value of n? The method of proof is the following. To prove a statement by induction, we must prove parts 1) and 2) above. Example 1. Proof. Mc ty pascal 2009 1. Sierpinski triangle. Generated using a random algorithm.
Swarm intelligence. Swarm intelligence (SI) is the collective behavior of decentralized, self-organized systems, natural or artificial. The concept is employed in work on artificial intelligence. The expression was introduced by Gerardo Beni and Jing Wang in 1989, in the context of cellular robotic systems.[1] The application of swarm principles to robots is called swarm robotics, while 'swarm intelligence' refers to the more general set of algorithms. 'Swarm prediction' has been used in the context of forecasting problems. Models of swarm behavior[edit] Boids (Reynolds 1987)[edit]
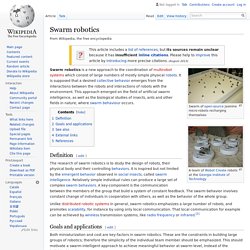
Swarm robotics. Swarm of open-source Jasmine micro-robots recharging themselves Swarm robotics is a new approach to the coordination of multirobot systems which consist of large numbers of mostly simple physical robots.
It is supposed that a desired collective behavior emerges from the interactions between the robots and interactions of robots with the environment. This approach emerged on the field of artificial swarm intelligence, as well as the biological studies of insects, ants and other fields in nature, where swarm behaviour occurs. Definition[edit] The research of swarm robotics is to study the design of robots, their physical body and their controlling behaviors. Unlike distributed robotic systems in general, swarm robotics emphasizes a large number of robots, and promotes scalability, for instance by using only local communication. Goals and applications[edit] How Search Works – Inside Search – Google. Pascal's Triangle. Patterns Within the Triangle Using Pascal's Triangle Heads and Tails Pascal's Triangle can show you how many ways heads and tails can combine.
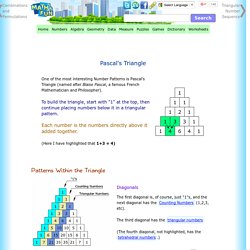
This can then show you the probability of any combination. For example, if you toss a coin three times, there is only one combination that will give you three heads (HHH), but there are three that will give two heads and one tail (HHT, HTH, THH), also three that give one head and two tails (HTT, THT, TTH) and one for all Tails (TTT). Example: What is the probability of getting exactly two heads with 4 coin tosses? There are 1+4+6+4+1 = 16 (or 24=16) possible results, and 6 of them give exactly two heads. Combinations The triangle also shows you how many Combinations of objects are possible. Example: You have 16 pool balls. Answer: go down to the start of row 16 (the top row is 0), and then along 3 places (the first place is 0) and the value there is your answer, 560.
Here is an extract at row 16: A Formula for Any Entry in The Triangle.