Jean Giraud 2 Un erratum Michel Langevin, l’un des tapirs de (l’ENS de) Saint-Cloud que j’ai évoqués dans la première partie de cet article, me signale que c’est Fulbert Mignot et non Maurice Mignotte qui fut l’un des autres tapirs. (J’appelle ici « tapir » ce que les normaliens de la rue d’Ulm semblent avoir appelé « caïman », c’est-à-dire un assistant préparateur ; je ne suis d’ailleurs pas certain que ce mot ait été usité à Saint-Cloud, mais c’est celui qui m’est venu.) Cet « incident » a été pour moi l’occasion (agréable) d’avoir de leurs nouvelles... Singularités encore La vie de Jean Giraud dans les années 70 et 80 est en partie liée à la résolution des singularités en caractéristique positive : c’est le cas par exemple de l’histoire de ses rapports avec « les mathématiciens espagnols » ; sans surcharger ce texte d’idées mathématiques, il est inévitable d’en parler un peu. Alexandre Grothendieck, Shreeram Abhyankar et Michael Artin. Heisuke Hironaka L’ENS de Lyon Jean Giraud
Jean Giraud 1 Jean Giraud est décédé le 27 mars 2007, à l’âge de soixante-et-onze ans, des suites d’une insuffisance pulmonaire grave, à l’hôpital de la Croix-Rousse à Lyon où il avait été amené en urgence. Giraud était connu de la communauté mathématique française pour (au moins) trois raisons assez différentes. La plus ancienne est son livre « Non Abelian Cohomology », tiré de sa thèse d’État préparée sous la direction d’Alexandre Grothendieck. Pour toutes ces raisons, et d’autres, Jean Giraud a marqué la mémoire de nombreux mathématiciens. Je ne peux que présenter l’excuse habituelle d’incompétence pour les faiblesses du texte qui va suivre. Une note personnelle : j’ai été un moment l’élève de Giraud ; la relation d’amitié et d’affection qui est venue ensuite en a été marquée et je n’ai jamais réussi (malgré son aide) à le tutoyer ni à l’appeler par son prénom. Famille et premières études JG est né le 2 février 1936 à Lyon cinquième ; puis il a habité à Sathonay-Camp. L’ENS d’Ulm Premier foyer
Edouard Jean-Baptiste Goursat ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Après des études secondaires à Brive (Corrèze), Goursat "monte" à Paris et sera élève au lycée Henri IV. A sa sortie de l'ENS (École normale supérieure), agrégé de mathématiques (1879, Goursat prépare et obtient son doctorat (Sur l'équation différentielle linéaire qui admet pour intégrale la série hypergéométrique, 1881) et enseigne alors à la faculté des sciences de Toulouse, proche de sa région natale (le Lot). Quatre ans plus tard, Goursat enseignera à l'ENS, à l'École polytechnique (1896), puis à la Sorbonne où il obtient une chaire de calcul différentiel et intégral (1897) succédant à Picard. La notion d'équation aux dérivées partielles : » Formes différentielles exactes ou non et intégration : » Afin de prouver son théorème selon lequel : Cauchy utilisa la condition de continuité de la fonction dérivée de f. ➔ Pour en savoir plus : Pearson Peano
René Gateaux ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Éléments biographiques/ portrait : Laurent Mazliak (CNRS), réf.1/ Exposition René Gateaux (ENS), réf.2 René Gâteaux naquit à Vitry le François, où naissait en 1667, un célèbre mathématicien français : Abraham de Moivre. Brillant élève, bachelier à l'âge de 15 ans, il entre trois ans plus tard à l'École Normale Supérieure de Paris en 1907 (il n'a que 18 ans...). Agrégé de mathématiques (1910), appelé sous les drapeaux, Gâteaux est nommé professeur de mathématiques au lycée de Bar-le-Duc. Sa passion pour les mathématiques et l'analyse fonctionnelle en particulier, le conduit à obtenir, sur la Jacques Hadamard, une bourse d'études à Rome où il rencontre Vito Volterra (tout comme son contemporain et compatriote Maurice Fréchet dix ans auparavant) alors spécialiste incontournable de cette branche mathématique en plein essor. Dérivée au sens de Gâteaux :
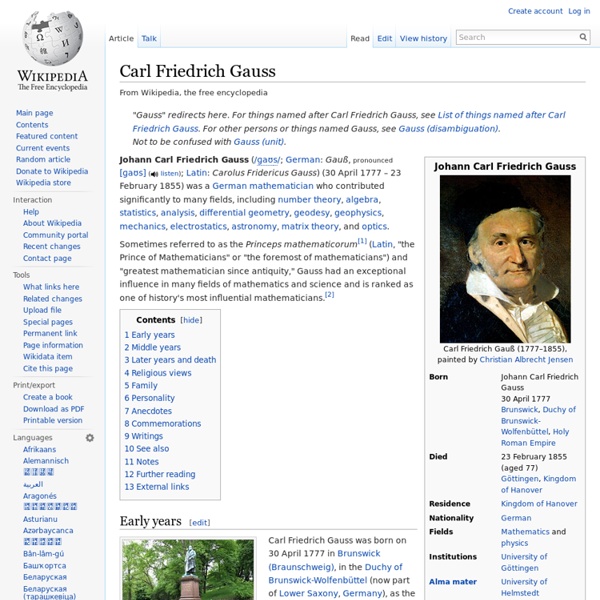
L'arithmétique de Gauss ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Une des contributions majeures de Gauss en mathématiques sera dans ses Recherches arithmétiques (Disquisitiones arithmeticae, 1801, disponibles en français sur Gallica (traduction de A.-C.-M. Poullet-Delisle,1807) où il crée une théorie arithmétique nouvelle avec le concept de congruence en énonçant des résultats et théorèmes fondamentaux. Il faut cependant noter que le concept implicite de congruence apparaît déjà en Grèce avec Diophante d'Alexandrie et en Inde avec Brahamagupta. ➔ L'intervention des structures algébriques, avec l'anneau Z/nZ des entiers modulo, l'étude des corps de nombres algébriques, les groupes de Galois, ... permettent de parler de théorie algébrique des nombres. Si a, b et p désignent des entiers relatifs on écrit a ≡ b [p] pour signifier que a - b est un multiple de p. On dit que a est congru à b modulo p. ∗∗∗1. Remarque :
Gauss (Gauß) Karl Friedrich ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Enfant prodige, né à Brunswick dans une famille pauvre, Gauss obtint une bourse (1792) du duc de Brunswick afin de poursuivre ses études. Il étudia à Göttingen de 1795 à 1798 et soutint sa thèse l'année suivante (1799) à Helmstedt sous la direction de Pfaff (qui devint son ami), portant sur une démonstration rigoureuse du fameux théorème de d'Alembert. Illustre mathématicien (arithmétique, géométrie différentielle), physicien (importants travaux et publications en électricité, optique et magnétisme, théorie du potentiel), Gauss fut aussi, et principalement, un astronome réputé. Il établit (1801) l'orbite de Cérès, découverte la même année par l'astronome italien Giuseppe Piazzi, en utilisant une méthode toute nouvelle : la méthode des moindres carrés (»ci-après). En savoir un peu plus sur ce célèbre théorème : » On dit que a est congru à b modulo p.
Galton Francis ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Physiologiste, anthropologue, météorologue (on lui doit le terme d'anticyclone), grand voyageur (explorateur en Afrique) et cousin de Charles Darwin (célèbre naturaliste, auteur de la théorie de l'évolution biologique : darwinisme). Galton est à l'origine de l'eugénisme (ou eugénique) : une théorie (très discutable...) fondée sur la recherche de méthodes scientifiques sélectives appliquées à la génétique et destinées (en principe...) à améliorer l'espèce animale ou humaine. » Auguste Bravais (français, 1811-1863), polytechnicien, officier de marine, professeur à l'Ecole polytechnique. Astronome, minéralogiste et explorateur, son nom est aussi associé aux réseaux cristallins qu'il a mis en évidence. Notions de statistique descriptive : » Régression & méthode des moindres carrés : » La loi normale, une loi bien naturelle Gauss et la loi normale : »
Gödel Kurt Friedrich ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Mathématicien et philosophe d'origine autrichienne, le plus grand logicien depuis Aristote, selon Von Neumann. Après avoir débuté des études de physique à Vienne, il se passionne pour la théorie des nombres en suivant les cours de Phillip Fürtwängler (1869-1940) -de la même famille que le célèbre chef d'orchestre Wilhelm Fürtwängler- et poursuit dès lors (1926) des études de mathématiques tout en s'intéressant à la philosophie. Sa thèse sur la complétude du calcul logique (über die Vollständigkeit des Logikkalcüls, 1929) est supervisée par Hahn à l'université de Vienne. Professeur en cette même université, c'est à 25 ans que Gödel énonça son célèbre théorème d'incomplétude. L'arrivée d'Hitler au pouvoir en 1933 va perturber la carrière du jeune mathématicien. » Tarski , Skolem , Henkin , Maltsev Aristote et logique aristotélicienne : » Gelfond Leray
Roger Godement Un article de Wikipédia, l'encyclopédie libre. Roger Godement en 1984. Biographie[modifier | modifier le code] Il a été un membre actif de Bourbaki au début des années 1950 et a donné beaucoup d'exposés au séminaire Bourbaki. Il a aussi participé au séminaire Cartan. Style et prises de positions politiques[modifier | modifier le code] Il a enseigné à l'université Paris VII dans les années 70 et 80. Roger Godement a toujours soutenu l'idée selon laquelle il était envisageable de transmettre les principaux concepts de base de l'Algèbre et de l'Analyse (voir l'introduction de son Cours d'Algèbre et les premières lignes de son cours d'Analyse) au plus grand nombre en des termes accessibles et pourtant rigoureux. Bibliographie[modifier | modifier le code] Topologie Algébrique et théorie des faisceaux, Hermann, 1960Cours d'Algèbre, Hermann, 1964Introduction à la théorie des groupes de Lie, Springer, 2004Analyse Mathématique, Springer, 2001 I. Notes et références[modifier | modifier le code]
vitrine Godement • version PDF GODEMENT Roger, Les fonctions de type positif et la théorie des groupes, Paris, [s.n.], 1946 GODEMENT Roger, CARTAN Henri, "Théorie de la dualité et analyse harmonique dans les groupes abéliens localement compacts" in Annales scientifiques de l’École normale supérieure (3), 64, 1947, p. 79-99 GODEMENT Roger, Topologie algébrique et théorie des faisceaux, Paris, Hermann, 1958 ("Actualités scientifiques et industrielles", 1252) GODEMENT Roger, "La formule des traces de Selberg considérée comme source de problèmes mathématiques" in Séminaire Bourbaki, 1, 1962-1963, exposé 244 GODEMENT Roger, Cours d’algèbre, Paris Hermann, 1963 GODEMENT Roger, Notes on Jacquet-Langlands’ theory, Princeton, Institute for advanced study, 1970 GODEMENT Roger, JACQUET Hervé, Zeta functions of simple algebras, Berlin, Springer, 1972 GODEMENT Roger, Analyse mathématiques. 1, Convergence, fonctions élémentaires, Berlin, Springer, 1998