Bienvenue sur Labomep Pi history - MacTutor History of Mathematics A little known verse of the Bible reads And he made a molten sea, ten cubits from the one brim to the other: it was round all about, and his height was five cubits: and a line of thirty cubits did compass it about. (I Kings 7, 23) The same verse can be found in II Chronicles 4, 2. A suggestion of how this could be interpreted to lead to a much better value is at THIS LINK. The fact that the ratio of the circumference to the diameter of a circle is constant has been known for so long that it is quite untraceable. The first theoretical calculation seems to have been carried out by Archimedes of Syracuse (287-212 BC). 71223<π<722. Before giving an indication of his proof, notice that very considerable sophistication involved in the use of inequalities here. Here is Archimedes' argument. Consider a circle of radius 1, in which we inscribe a regular polygon of 3×2n−1 sides, with semiperimeter bn, and superscribe a regular polygon of 3×2n−1 sides, with semiperimeter an. a1,a2,a3,...
Exercices avec Scratch en troisième [3ème], programmation et algorithme. Scratch en troisième (3ème) au cycle 4 avec de nombreux exercices de programmation et d’algorithme.Les élèves peuvent s’exercer en ligne en manipulant les différents blocs du logiciel scratch mais également en effectuant des boucles, en créant des variables.Ces exercices peuvent être traités au niveau cycle 4 en collège. Exercice 1 Associer chaque programme à la sortie correspondante. Exercice 2 Ce code figure sur le lutin arrow Que fait ce lutin lorsque le programme est éxécuté ? Exercice 3 Que fait ce programme ? Exercice 4 On a éxécuté ce programme et on a saisi le nombre 45. Quel est le contenu de ma liste à la fin de l’éxécution ? Exercice 5 Comment compléter ce programme afin de pouvoir ajouter le nombre saisi à la liste seulement dans le cas où le nombre n’y figure pas encore ? Exercice 6 Quel code faut-il ajouter sur les deux lutins afin que le lutin Bear1 dise bonjour au chat une fois ce dernier près de lui ? Exercice 7 On clique sur le chat. Exercice 8 La scène comporte un lutin Ball. Exercice 9
Histoires autour de la salle Pi - visite générale - version française 1 - Rio, le Louvre et la Salle Pi par Pierre AUDIN Lire la transcription de l'audio 01Fermer la transcription de l'audio 01 1 - Rio, le Louvre et la Salle Pi par Pierre AUDINBonjour. Un dimanche soir, je me dirige vers mon bureau auquel j’accède par la Salle Pi. Tout le monde à Rio sait qu’au Louvre il y a une Salle Pi. Bravo le Louvre ! 2 - Qu'est ce que le nombre Pi ? Lire la transcription de l'audio 02Fermer la transcription de l'audio 02 2 - Qu'est ce que le nombre Pi ? Le nombre Pi est associé au cercle, ce qui justifie la forme cylindrique de cette salle. Pour percevoir concrètement où se trouve Pi dans un cercle, dirigez-vous vers l’unique manipe située à gauche en entrant dans la salle. Vérifiez pour commencer que la distance entre deux nœuds est à peu près égale au diamètre du disque correspondant. Cela vient du fait que tous les cercles ont une même forme : ils sont tous un agrandissement ou une réduction d’un autre, sans déformation. 5 - Pi est-il un "nombre univers" ?
Swirly hexagon 6 color PNG Clip arts for Web - Clip arts free PNG Backgrounds swirly hexagon 6 color clipart vector file with svg. This free Clip arts design of Swirly hexagon 6 color PNG Clip arts has been published by Clipartsfree.net. The origional size of the image is 900 × 900 px and the original resolution is 300 dpi. Thousands ClipartsFree users have previously viewed this image, from photographs free collection on ClipartsFree. The source also offers Clip arts photographs free: swirly, hexagon, 6, color, File Bytes: 4877 bytes Share Link Copy Embed in HTML <a href=" title="Swirly hexagon 6 color" target="_blank"><img src=" alt="Swirly hexagon 6 color PNG image" /><br />Swirly hexagon 6 color PNG Clip arts</a> Licencing!
Théorème d'Hermite-Lindemann Un article de Wikipédia, l'encyclopédie libre. Le théorème d’Hermite-Lindemann affirme que pour tout nombre algébrique a non nul, le nombre ea est transcendant. Il fut démontré en 1882 par Ferdinand von Lindemann[1]. En 1885, Karl Weierstrass en donna une généralisation, connue sous le nom de théorème de Lindemann-Weierstrass. Une généralisation plus récente est le théorème de Baker. Transcendance de e et π[modifier | modifier le code] En particulier, e est transcendant (résultat montré par Charles Hermite en 1873[2] : c’est le théorème d’Hermite). La transcendance de π est aussi un corollaire du théorème de Lindemann : sin(π) = 0, or on déduit plus généralement du théorème la transcendance de tout nombre non nul t dont (par exemple) le sinus est algébrique. L'approche originelle d'Hermite pour e a été simplifiée et étendue à π par David Hilbert (en 1893)[3],[4], pour finalement devenir élémentaire grâce à Adolf Hurwitz et Paul Albert Gordan. Notes et références[modifier | modifier le code]
Pavage de Penrose L'univers de Pi - Lindemann Transcendance de e :Soit f(x) un polynôme de degré m à coefficients réels. Posons : On intègre m fois par parties et on obtient alors : Maintenant, soit f* le polynôme f où les coefficents ont été remplacés par leur valeur absolue. En majorant les termes dans l'intégrale, on obtient : Ces préliminaires étant écrites, recentrons le débat et supposons e algébrique. avec toujours m=(n+1)p-1.
Pavages du plan avec des losanges Pavages du plan avec des losanges 120°-60° Si l'on fait un empilement semi-régulier de cubes par translations et que l'on projette cylindriquement sur un plan parallèlement à une diagonale du cube élémentaire, on obtient un pavage de ce plan avec des losanges 120°-60°. Quelques exemples : on peut considérer que c'est un empilement vu par-dessus ou un empilement vu par-dessous Les images de droite sont les pavages correspondants du plan. Les images de gauche sont des anaglyphes ; si on les regarde avec des lunettes rouge-cyan, on voit en relief, sans ambiguitë, la vue de dessus. Si on les regarde sans lunettes, on peut voir soit la vue de dessus soit la vue de dessous en se concentrant sur une face bleue d'un cube que l'on considère comme soit la face supérieure soit la face inférieure puis on élargit la vision au reste de l'image.
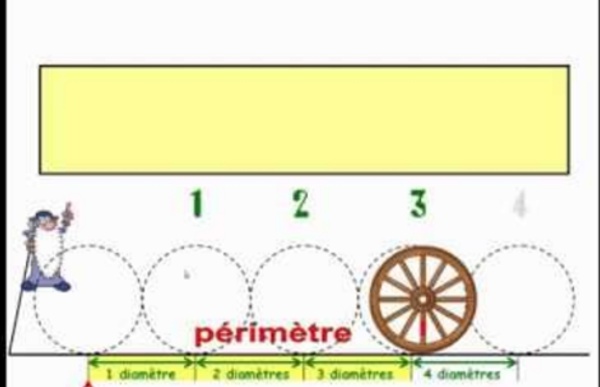
Images des mathématiques Vous avez sans doute entendu parler du nombre qui intervient dans les formules que l’on apprenait à l’école élémentaire : pour le périmètre du cercle de rayon et pour l’aire délimitée par ce cercle (actuellement cela s’apprend en CM2 pour le périmètre et en 6ième pour l’aire). Je me souviens aussi des valeurs approchées ( ou ou ) de ce nombre que j’ai apprises au CM1 au cours d’une leçon qui m’a marqué pour la vie. Notre instituteur nous apprit ainsi que le nombre permet de calculer le périmètre de tous les cercles, quel que soit leur rayon, et aussi l’aire des disques qu’ils délimitent. Le plus impressionnant pour moi fut d’apprendre que ce nombre a une infinité de décimales et que personne ne peut en donner la liste ni la décrire. Le nombre a une infinité de décimales et ce sont toutes des 3 ; la suite des décimales du nombre est facile à décrire : à partir de la cinquième décimale on juxtapose des blocs identiques . Naissance des mathématiques européennes : la Grèce Vers 600 av.
Photocopier, colorier et coller des feuilles A4 pour créer des affiches présentant le périmètre, l'aire et le volume de figures et solides usuels (collège et formation professionnelle) Présentation Créer très facilement des affiches pédagogiques à fort impact visuel. Exposer ces affiches (4 tailles possibles) en salle de cours et dans la chambre des élèves. 1. Photocopier un certain nombre de feuilles A4 noir et blanc (30 feuilles au total). 2. 3. Ces différentes affiches peuvent être créées avec : 16 feuilles A4. Visualiser les affiches créées avec 16 feuilles A4, 8 feuilles A4, 4 feuilles A4 et 2 feuilles A4. Imprimer quelques feuilles A4 au format PDF et les afficher à un mur pour se rendre compte de leur impact. Imprimer une feuille A4 (affiche créée avec 16 feuilles A4). Imprimer une feuille A4 (affiche créée avec 8 feuilles A4). Imprimer une feuille A4 (affiche créée avec 4 feuilles A4). Remarque : Certains navigateurs (Mozilla Firefox ...) ont développé des lecteurs de fichiers PDF intégrés. Fiche technique