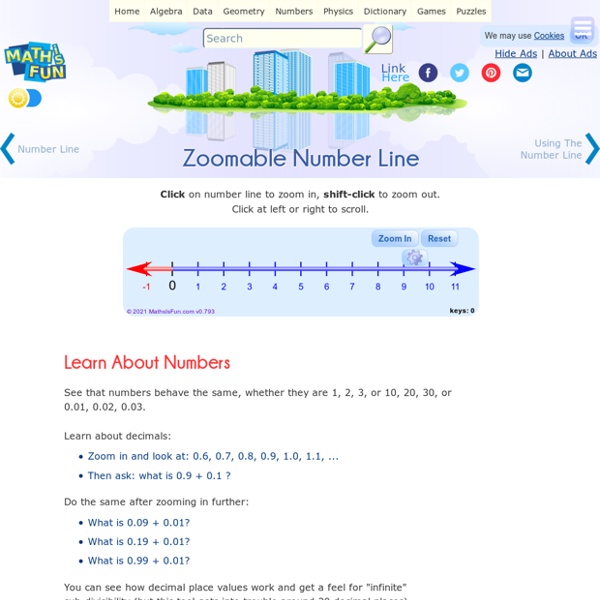
Interactive Number Line Generator
Got it! This website uses cookies to ensure you get the best experience on our website More info Cookie Consent plugin for the EU cookie law
How folding paper can get you to the moon - Adrian Paenza
The exponential growth that Paenza plays with is hypothetical, but real-world exponential growth patterns exist all around us—in microbiology, economics, public health, and technology, to name just a few. Identify some instances of exponential growth in one or more of these domains. Working with classmates, create an exhibit for younger students that defines exponential growth, shares real-world examples, and suggests simple experiments that they can do in order to see exponential growth in action.Assume that you’re working with a piece of paper that’s 0.001 cm thick, as Paenza proposes, and one meter on each side. At what point will you be unable to fold the paper anymore because its thickness has exceeded the area available for folding? Adriàn Paenza: Matematica, Estas Ahi? IBM’s Mathematics Peepshow: Legend of the Chessboard
Arbeta med tallinjen
I mitt förra blogginlägg berättade jag att jag testat mina elever med det nya bedömningsstödet i taluppfattning som Skolverket kom ut med i somras. När jag utvärderade resultaten visade det sig att det var framför allt två områden jag behövde fokusera mer på. Det ena var att träna eleverna att skriftligt redovisa sina lösningar (vilket jag skrev om i förra inlägget) och det andra var att öva på tallinjen. I detta inlägg tänkte jag därför dela med mig av lite tips och övningar som förhoppningsvis kan hjälpa elever som har svårt med just tallinjen. Det finns flera forskare som vittnar om tallinjens betydelse för matematikinlärning. En av dem är Torkel Klingberg, professor i kognitiv neurovetenskap vid Karolinska institutet i Stockholm.
Fredriks lektioner når miljonpublik
Det är kvällstid i villaområdet i Lindesberg. Tisdagens arbetsdag har sedan länge avslutats för de alla flesta. Men inte för läraren Fredrik Lindmark.
Maths Starters and Quick Practice on Mr Barton Maths
arrow_back Back to Teachers Maths Starters, Quick Practice and Cover Work The following resources are absolutely ideal. Each of the links here share two wonderful things in common: you can generate an infinite number of questions, and you get all the answers.
Framgångsrik modell gör matten tydlig
Alla elever som släntrar in i det lilla klassrummet på Carlssons skola i Stockholm är införstådda med att de ska arbeta med räknemetoden som kallas blockmodellen. Stämningen är lite stökig. En av eleverna skämtar med hög röst, men läraren Cecilia Christiansen lyckas skapa ett lugn genom en kort och skarp kommentar: – Vet du vad … de andra har rätt att ha en lektion som vanligt. När jag kom hem kände jag mig helt lycklig, med känslan ’nu vet jag hur vi ska lyfta matematiken’. Blockmodellen är en av många delar i den reform som revolutionerade matematikundervisningen i Singapore i början på 1990-talet, då man implementerade en ny kursplan.
Free First Grade Math Worksheets: Number Sense, Addition, Rounding
Welcome to the first grade math page at TLSBooks. This page features first grade math activities related to number sense, addition, rounding, and estimation practice. Subsequent first grade math pages include subtraction and mixed operations and geometry and measurement. First grade is an extremely important year in the mathematical development of your child. By the end of this year they should have the ability to skip count past 100, read and write numbers to 100 (or preferably to 1,000), and represent a number of objects with a written numeral. First graders should continue working with patterns in an effort to improve problem solving skills.
Introducera algebra
Var uppstod behovet av att använda variabler i matematik? Började man använda bokstäver (eller andra symboler) för att beteckna ett okänt tal eller för att beskriva ett samband? Eller kanske något helt annat? I vilken situation upptäcktes värdet av att använda symbolerna?
Malins PPlugg
Då har jag påbörjat planeringen av matematikundervisningen inför höstterminen. Jag bestämde mig ju för att jag skulle äga matematikplaneringen inför de nationella proven i våras så nu ska det bli verklighet är tanken. Jag ska göra en pedagogisk planering och en PP-vägg som jag använder på riktigt i undervisningen så som jag gör i svenska, So och No. Så efter att funderat på vad jag har att rätta mig efter har jag snickrat ihop en alignmentplanering för höstterminen. Vad är det vi ska lära oss?
10 fakta du antagligen inte visste om pi – 10fakta.se
Vi kan aldrig riktigt mäta omkretsen eller arean av en cirkel, eftersom vi aldrig riktigt vet värdet av pi. Pi är ett irrationellt tal, vilket innebär att dess siffror går på för evigt i en till synes slumpmässig sekvens. Om du inte fått nog av pi i skolan kan du här ta del av tio fakta som du gissningsvis inte redan kände till. 01) I Star Trek-avsnittet “Wolf in the Fold” lurar och besegrar Spock den onda datorn genom att säga till honom att räkna upp den sista siffran i pi. 02) Symbolen för pi (π) har bara använts regelbundet i matematiska syften under de senaste 250 åren. 03) I det grekiska alfabetet, är “π” (piwas) den sextonde bokstaven.
LÄTT ATT LÄRA!
Tycker ditt barn att det är tråkigt att träna på multiplikationstabellen och de andra räknesätten? Här hittar du massor av roliga länkar, till övningar och roliga mattespel! Klicka nedan på den blåfärgade texten för att komma till önskat område. Du och ditt barn kommer inte att bli besvikna! Det finns även lite länkar till spel och övningar om klockan. Matematik