


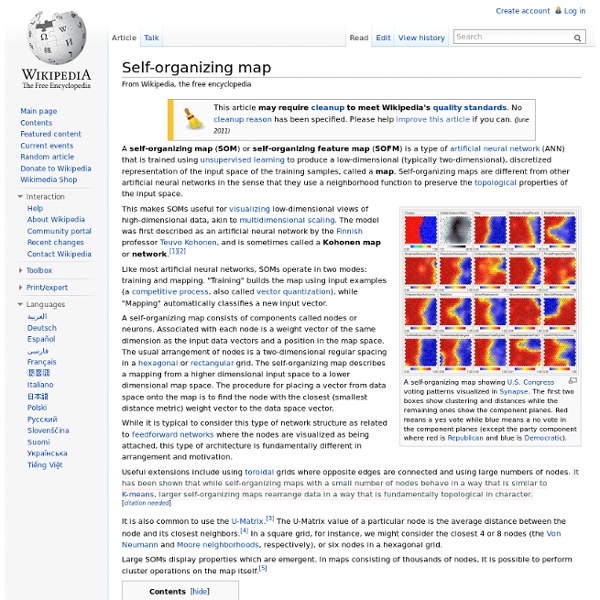
Multilayer perceptron A multilayer perceptron (MLP) is a feedforward artificial neural network model that maps sets of input data onto a set of appropriate outputs. A MLP consists of multiple layers of nodes in a directed graph, with each layer fully connected to the next one. Except for the input nodes, each node is a neuron (or processing element) with a nonlinear activation function. Theory[edit] Activation function[edit] If a multilayer perceptron has a linear activation function in all neurons, that is, a linear function that maps the weighted inputs to the output of each neuron, then it is easily proved with linear algebra that any number of layers can be reduced to the standard two-layer input-output model (see perceptron). The two main activation functions used in current applications are both sigmoids, and are described by in which the former function is a hyperbolic tangent which ranges from -1 to 1, and the latter, the logistic function, is similar in shape but ranges from 0 to 1. Layers[edit] in the
Connectionism Connectionism is a set of approaches in the fields of artificial intelligence, cognitive psychology, cognitive science, neuroscience, and philosophy of mind, that models mental or behavioral phenomena as the emergent processes of interconnected networks of simple units. There are many forms of connectionism, but the most common forms use neural network models. Basic principles[edit] The central connectionist principle is that mental phenomena can be described by interconnected networks of simple and often uniform units. Spreading activation[edit] In most connectionist models, networks change over time. Neural networks[edit] Neural networks are by far the most commonly used connectionist model today.Though there are a large variety of neural network models, they almost always follow two basic principles regarding the mind: Most of the variety among neural network models comes from: Biological realism[edit] Learning[edit] By formalizing learning in such a way, connectionists have many tools.
Protein Secondary Structure Prediction with Neural Nets: Feed-Forward Networks Introduction to feed-forward nets Feed-forward nets are the most well-known and widely-used class of neural network. The popularity of feed-forward networks derives from the fact that they have been applied successfully to a wide range of information processing tasks in such diverse fields as speech recognition, financial prediction, image compression, medical diagnosis and protein structure prediction; new applications are being discovered all the time. In common with all neural networks, feed-forward networks are trained, rather than programmed, to carry out the chosen information processing tasks. The feed-forward architecture Feed-forward networks have a characteristic layered architecture, with each layer comprising one or more simple processing units called artificial neurons or nodes. Diagram of 2-Layer Perceptron Feed-forward nets are generally implemented with an additional node - called the bias unit - in all layers except the output layer. Training a feed-forward net 1. 2. 3.
Restricted Boltzmann machine Diagram of a restricted Boltzmann machine with three visible units and four hidden units (no bias units). A restricted Boltzmann machine (RBM) is a generative stochastic neural network that can learn a probability distribution over its set of inputs. RBMs were initially invented under the name Harmonium by Paul Smolensky in 1986,[1] but only rose to prominence after Geoffrey Hinton and collaborators invented fast learning algorithms for them in the mid-2000s. RBMs have found applications in dimensionality reduction,[2] classification,[3] collaborative filtering, feature learning[4] and topic modelling.[5] They can be trained in either supervised or unsupervised ways, depending on the task. Restricted Boltzmann machines can also be used in deep learning networks. Structure[edit] associated with the connection between hidden unit and visible unit , as well as bias weights (offsets) for the visible units and for the hidden units. or, in vector form, where visible units and and See also[edit]
Feature learning Feature learning or representation learning[1] is a set of techniques in machine learning that learn a transformation of "raw" inputs to a representation that can be effectively exploited in a supervised learning task such as classification. Feature learning algorithms themselves may be either unsupervised or supervised, and include autoencoders,[2] dictionary learning, matrix factorization,[3] restricted Boltzmann machines[2] and various form of clustering.[2][4][5] When the feature learning can be performed in an unsupervised way, it enables a form of semisupervised learning where first, features are learned from an unlabeled dataset, which are then employed to improve performance in a supervised setting with labeled data.[6][7] Clustering as feature learning[edit] K-means clustering can be used for feature learning, by clustering an unlabeled set to produce k centroids, then using these centroids to produce k additional features for a subsequent supervised learning task. See also[edit]
Recurrent neural network A recurrent neural network (RNN) is a class of neural network where connections between units form a directed cycle. This creates an internal state of the network which allows it to exhibit dynamic temporal behavior. Unlike feedforward neural networks, RNNs can use their internal memory to process arbitrary sequences of inputs. Architectures[edit] Fully recurrent network[edit] This is the basic architecture developed in the 1980s: a network of neuron-like units, each with a directed connection to every other unit. For supervised learning in discrete time settings, training sequences of real-valued input vectors become sequences of activations of the input nodes, one input vector at a time. Hopfield network[edit] The Hopfield network is of historic interest although it is not a general RNN, as it is not designed to process sequences of patterns. A variation on the Hopfield network is the bidirectional associative memory (BAM). Elman networks and Jordan networks[edit] The Elman SRN Where:
Feedforward neural network In a feed forward network information always moves one direction; it never goes backwards. A feedforward neural network is an artificial neural network where connections between the units do not form a directed cycle. This is different from recurrent neural networks. The feedforward neural network was the first and simplest type of artificial neural network devised. Single-layer perceptron[edit] The simplest kind of neural network is a single-layer perceptron network, which consists of a single layer of output nodes; the inputs are fed directly to the outputs via a series of weights. A perceptron can be created using any values for the activated and deactivated states as long as the threshold value lies between the two. Perceptrons can be trained by a simple learning algorithm that is usually called the delta rule. A multi-layer neural network can compute a continuous output instead of a step function. (times , in general form, according to the Chain Rule) Multi-layer perceptron[edit]
Artificial neural network An artificial neural network is an interconnected group of nodes, akin to the vast network of neurons in a brain. Here, each circular node represents an artificial neuron and an arrow represents a connection from the output of one neuron to the input of another. For example, a neural network for handwriting recognition is defined by a set of input neurons which may be activated by the pixels of an input image. After being weighted and transformed by a function (determined by the network's designer), the activations of these neurons are then passed on to other neurons. Like other machine learning methods - systems that learn from data - neural networks have been used to solve a wide variety of tasks that are hard to solve using ordinary rule-based programming, including computer vision and speech recognition. Background[edit] There is no single formal definition of what an artificial neural network is. History[edit] Farley and Wesley A. Recent improvements[edit] Models[edit] or both and , where
Autoencoder An autoencoder, autoassociator or Diabolo network[1]:19 is an artificial neural network used for learning efficient codings.[2] The aim of an auto-encoder is to learn a compressed, distributed representation (encoding) for a set of data, typically for the purpose of dimensionality reduction. Overview[edit] Architecturally, the simplest form of the autoencoder is a feedforward, non-recurrent neural net that is very similar to the multilayer perceptron (MLP), with an input layer, an output layer and one or more hidden layers connecting them. For each input x, Do a feed-forward pass to compute activations at all hidden layers, then at the output layer to obtain an output x̂ Measure the deviation of x̂ from the input x (typically using squared error, i) Backpropagate the error through the net and perform weight updates. (This algorithm trains one sample at a time, but batch learning is also possible.) Auto-encoders can also be used to learn overcomplete feature representations of data.