


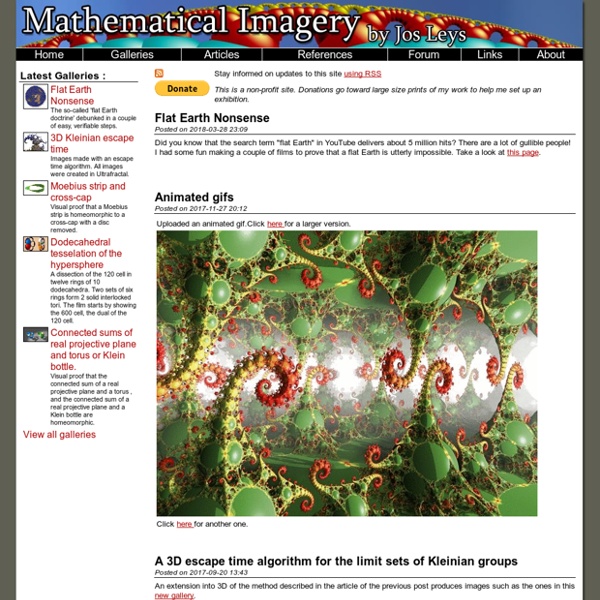
Images des mathématiques Piste verte Le 26 juillet 2016 - Ecrit par Jos Leys Les ensembles de Julia sont parmi les exemples les plus célèbres d’ensembles fractals. On se fixe un nombre complexe et on considère alors l’ensemble des points du plan complexe qui ne partent pas vers l’infini sous l’action répétée de la transformation . Rediffusion d’un article du 17 juin 2013. Pour en savoir plus, voir cet article. En ajoutant une profondeur à la zone en dehors de l’ensemble on crée des montagnes, comme dans ce film : Partager cet article Pour citer cet article : Jos Leys — «Un vol au dessus des montagnes de Julia» — Images des Mathématiques, CNRS, 2016 Abundant Earth Environmental SuperStore Par Michèle Audin et Arnaud Chéritat: les ensembles limites Au cours d’une étude historique des travaux de Fatou et Julia sur l’itération des fractions rationnelles, l’une des auteurs de cet article (que nous désignerons par la lettre M, nous utiliserons la lettre A pour désigner l’autre auteur) s’intéresse à l’histoire des images, images d’« ensembles de Julia » notamment. C’est une idée courante qu’il a fallu attendre l’arrivée des ordinateurs pour voir apparaître, déferler même, des images d’ensemble de Julia. C’est vrai du déferlement, voire de la publication de ces images, mais ce n’est pas vrai de leur existence, puisque Gaston Julia [1] lui-même avait dessiné, dès 1917, un ensemble « de Julia » tout à fait réaliste sur un de ses manuscrits [2]. Vous avez sans doute déjà vu des images de ce genre [3]. Précisons qu’il n’est besoin de savoir, ni ce qu’est un ensemble de Julia, ni ce qu’est un ensemble-limite, pour lire cet article ! Feuilletage, donc, par M, des onze volumes des Œuvres de Poincaré. De quoi s’agit-il ? Il y en a cinq.
Marshall Kirkpatrick » 10 ways to make remembering to read your After building a rockin’ good OPML file for a client last month a classic problem has come up that I want to write about here: how do you stay motivated to read your feeds regularly? I subscribe to far more feeds than most people (3,000+) and am able to stay on top of them well enough. Here are some ways I do it, as well as some thoughts from some friends. Some of these are pretty standard but I hope that at least some are new to you. Please leave a comment if you can suggest other methods – I’d really like to be able to articulate ways we can prevent the all-too-common “info overload” backlash that’s leading many people to lose out on a lot of the potential offered by new web tools. Organize by priority I have two folders in my feedreader, one for high priority feeds that I try to scan at least once a day and one bulk folder for feeds that I get to when and if I can. Use a river of news Scan for things to read RSS is not email. Use other methods for “can’t miss news” Fear falling behind
Les fractales | Dossier Définir correctement ce qu'est une fractale n'est pas simple et certaines définitions trouvées dans divers articles sont inexactes. Benoît MandelbrotBenoît Mandelbrot lui-même a varié dans ses propos : « "objet fractal" et "fractale", termes que je viens de former, pour les besoins de ce livre, à partir de l'adjectif latin fractus, qui signifie "irrégulier ou brisé". Fractale. n.f. Configuration fractale. Ensemble ou objet fractal ». Le terme « fractale » est un néologisme créé par le mathématicienmathématicien Benoît Mandelbrot en 1974 à partir de la racine latine fractus, qui signifie brisé, irrégulier. Des formes fractales approximatives sont facilement observables dans la nature. Dans ce dossier, nous verrons que les fractales sont plus fréquentes, autour de nous, dans la nature que les objets lisses. À lire aussi dans Futura :
Marshall Kirkpatrick » A post about some of my favorite tools: G My friend Justin Kistner has started a blog carnival of sorts that he’s calling Advanced Operators, all about working with new tools online. He’s had smart people contribute posts on all kinds of topics on their blogs and I thought I’d participate in this round. The topic this week is “my favorite tools.” Gmail RSS Did you know that you can get the contents of your Gmail inbox or just items with a particular filter or tag delivered via RSS? Just add a URL like this to your feed reader: where the word label is replaced with your label in GMail. Why would you want to do this? The other circomstance in which I’ve done this is to create a special section of my startpage to remind me of certain emails. FeedYes Speaking of feed creation, if you’ve got a webpage you want a feed from FeedYes is a great way to scrape one. What FeedYes does is ask you to provide a webpage’s URL, then it lists all the links on that page. FeedDigest
UNE BALADE PARMI LES ENSEMBLES DE JULIA Mon domaine de recherche principal abonde de noms imagés. J’aimerais vous montrer quelques exemples. La dynamique holomorphe est une branche des mathématiques un peu à part. D’une part, c’est une sous-branche des systèmes dynamiques, domaine où l’on peut étudier le comportement à long terme des orbites des planètes par exemple. D’autre part, les systèmes que je regarde ne correspondent à rien de réel. Qu’est-ce qui motive alors l’énergie que mes collègues et moi y consacrons ? ... qu’avons-nous ? En vrac : chou-fleur, lapin, éléphants, papillons, hippocampes, citron, dragons, monstre abyssal, aéroplane, koalas, Kokopelli, basilique, dendrites, batteur à œufs, bouquet, tapis, tamis, et plein d’autres... Allez, je vous fais faire un petit tour, puis commenterai un peu les usages en mathématiques. Le lapin de Douady. Probablement le plus célèbre des ensembles de Julia. Les ensembles de Julia, je ne vais pas vous les définir ici. Système dynamique : le lapin a même son film ! c = 0.25 c = 0.3
Findory Findory was a personalized news site. The site launched in January 2004 and shut down November 2007. A reader first coming to Findory would see a normal front page of news, the popular and important news stories of the day. Below is a screenshot of an example personalized Findory home page. [Clicking on the screenshot will bring up a full-sized version] Findory's personalization used a type of hybrid collaborative filtering algorithm that recommended articles based on a combination of similarity of content and articles that tended to interested other Findory users with similar tastes. One way to think of this is that, when a person found and read an interesting article on Findory, that article would be shared with any other Findory readers who likely would be interested. Findory's primary product was in news, but the broader goal of Findory was to personalize information. Video, podcast, and feed recommendations worked much like the news recommendations.
Fractals fractals Dans cette image, des milliards de mondes... images: Syti.net En vidéo, quelques zooms dans le fractal de Mandelbrot... Vanishing Point: How to disappear in America without a trace Where there's water, life is possible. True, it may be very difficult and very hard to live, depending, but anyone who's driven, hiked, or camped in the American South West will have noticed that cities and ranches crop up where there's surface water or where there's been a well dug. Within the state of California, Nevada, Arizona, Utah, New Mexico, and Colorado, there are deserts, mesas, mountains, and forests where normally people never or rarely visit; not-so-secret places where there's water, access to a road within a day's hike, and where a fairly rugged individual may hide while remaining basically healthy, marginally well fed, and reasonably sane. In this section I'll look at two such environments, neither of which I would recommend, but one of which I'd suggest is a reasonable way to live in basic health while either on the run, hiding out from the law, old girl friends, the draft for an illegal war, putative wives and such. Where exactly? How I Would Do It Some Other Areas
1980s Pop Song Reveals Fractal Rhythms of the Human Mind — NOVA Next Pop music in the 1980s was full of weirdness, but no amount of Madonna or “The Safety Dance” will prepare you for what scientists recently found in a Michael McDonald song—fractals. Physicist Holger Henning and colleagues at the Max Planck Institute for Dynamics and Self-Organization in Göttingen, Germany found self-similar patterns in the drum pattern of a recording of the 80s hit song “I Keep Forgettin’.” This pop classic features drummer Jeff Parcoro, who was a member of Toto and has played for other big names like Steely Dan, Madonna, and Pink Floyd. The music video for Michael McDonald’s "I Keep Forgettin’ You." Loosely speaking, a fractal pattern is distinctly recognizable no matter how much you zoom in or out, a property known as self-similarity. For example, if you show a pattern to a person looking through a microscope and to an astronaut looking down from orbit with a telescope, and they describe the same thing, then that pattern is self-similar.