

Differential Calculus of Functions of One Variable. Simple Book Publishing. A course in mathematical analysis. Differential Calculus. Calculus Unlimited - CaltechAUTHORS. Marsden, Jerrold and Weinstein, Alan J. (1981) Calculus Unlimited.

Benjamin/Cummings Publishing Company, Inc. , Menlo Park, CA. ISBN 0-8053-6932-5. Use this Persistent URL to link to this item: BC Exams: Free Response Question practice problems. Worldwide Single-Variable Calculus for AP® MATH 2500 (Calculus 1) Summer 2016. Math 2500 (Calculus 1) Sample Problems. Marco Learning Systems - Home Page. Calculus: early transcendentals. By Department of Mathematics Whitman College This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License.

To view a copy of this license, visit or send a letter to Creative Commons, 543 Howard Street, 5th Floor, San Francisco, California, 94105, USA. If you distribute this work or a derivative, include the history of the document. This text was initially written by David Guichard. The book includes some exercises and examples from Elementary Calculus: An Approach Using Infinitesimals, by H. This HTML version was produced by David Farmer, Albert Schueller, and David Guichard. Calculus: early transcendentals. World Web Math: Calculus Index. Mathematics 1A (Calculus) Math 2B: Calculus. Math 2A: Calculus.
Concepts In Calculus II. Gainesville, FL: University Press of Florida, 1232011. Concepts In Calculus I, Second Edition. Gainesville, FL: University Press of Florida, 822011. Calculus, with analytic geometry. Catalog Record: Calculus, with analytic geometry | Hathi Trust Digital Library Navigation HathiTrust Digital Library Search this index Main Content Similar Items Introduction to functional analysis.
Tools Calculus, with analytic geometry. Viewability: Full view (original from University of California) Full view (original from University of California) Search Catalog Search Bibliographic search (Title, Author, Subject, ISBN/ISSN, Publisher, Series Title, or Year of Publication) of all HathiTrust items Experimental Search Full-text search of a small subset of HathiTrust items Build & View Custom Collections Go to Public Collections to browse other people's collections. Full-text searching is available within public or private collections, and within individual items. Close Search Tips Phrase Searching Use quotes to search an exact phrase: e.g.
Wildcards Use * or ? Boolean Searching Use AND and OR between words to combine them with Boolean logic: e.g. Find your partner institution: Calculus, with analytic geometry.
The Circular Function/The Definite Integral. Differentiation. Differentiability implies continuity. Supporting and promoting the learning of mathematics everywhere. The Oxford Math Center. Calculus. APEX Calculus. Differential Calculus. Calculus Help. Applications Of Derivatives. Binomial theorem. The binomial coefficient appears as the bth entry in the nth row of Pascal's triangle (counting starts at 0). Each entry is the sum of the two above it. The coefficient a in the term of a xb yc is known as the binomial coefficient or (the two have the same value). Is often pronounced as "n choose b". History[edit] Special cases of the binomial theorem were known since at least the 4th century BC when Greek mathematician Euclid mentioned the special case of the binomial theorem for exponent 2.[1][2] There is evidence that the binomial theorem for cubes was known by the 6th century in India.[1][2] Binomial coefficients, as combinatorial quantities expressing the number of ways of selecting k objects out of n without replacement, were of interest to ancient Indian mathematicians. ,[4] and a clear statement of this rule can be found in the 12th century text Lilavati by Bhaskara.[4] In 1544, Michael Stifel introduced the term "binomial coefficient" and showed how to use them to express in terms of .
Derivative. Operation in calculus The graph of a function, drawn in black, and a tangent line to that function, drawn in red.
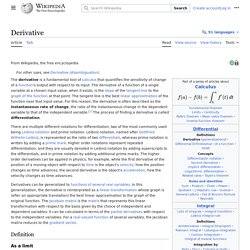
The slope of the tangent line is equal to the derivative of the function at the marked point. The derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. Slope. Slope: Slope is calculated by finding the ratio of the "vertical change" to the "horizontal change" between (any) two distinct points on a line.
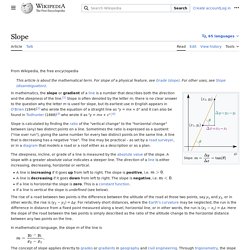
Sometimes the ratio is expressed as a quotient ("rise over run"), giving the same number for every two distinct points on the same line. MIT 18.01 Single Variable Calculus, Fall 2006. Calculus Online Textbook. Calculus.
Series And Sequences.