

Youtube. Youtube. Circle Geometry. Assumed knowledge Introductory plane geometry involving points and lines, parallel lines and transversals, angle sums of triangles and quadrilaterals, and general angle-chasing.

Experience with a logical argument in geometry written as a sequence of steps, each justified by a reason. Ruler-and-compasses constructions. The four standard congruence tests and their application to proving properties of and tests for special triangles and quadrilaterals. The four standard similarity tests and their application. Motivation Most geometry so far has involved triangles and quadrilaterals, which are formed by intervals on lines, and we turn now to the geometry of circles. The theorems of circle geometry are not intuitively obvious to the student, in fact most people are quite surprised by the results when they first see them. The theoretical importance of circles is reflected in the amazing number and variety of situations in science where circles are used to model physical phenomena.
Content POQ. The alternate segment theorem - Higher - Circle theorems - Higher - Edexcel - GCSE Maths Revision - Edexcel - BBC Bitesize. Circle Theorems. Inscribed Polygons and Circumscribed Polygons, Circles - Geometry. Power Theorems - Chords, Secants & Tangents - Circle Theorems - Geometry.
Tangent lines to circles. Inscribed angles. Circle theorems - Higher - Edexcel - Revision 8 - GCSE Maths - BBC Bitesize. Intersecting Chords Theorem. Category:Circles. Circles. ParallelAngleBisector The figure above shows a circle with two chords intersecting.
Circle Geometry Properties. Brilliant Today Courses Practice Sign up Log in Excel in math and science Master concepts by solving fun, challenging problems.
It's hard to learn from lectures and videos Learn more effectively through short, interactive explorations. Used and loved by over 7 million people Learn from a vibrant community of students and enthusiasts, including olympiad champions, researchers, and professionals. Incircle of Triangle. In the above diagram, circle O of radius 3 is inscribed in △ABC.
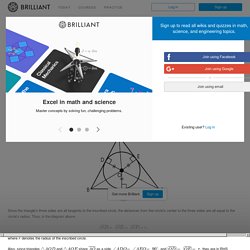
If the perimeter of △ABC is 30, what is the area of △ABC? The area of a circumscribed triangle is given by the formula 21×r×(the triangle’s perimeter), where r is the inscribed circle's radius. Therefore the answer is 21×3×30=45. SAT Circles. In the figure above, the circles are concentric, points X,Y,O,D, and C are collinear, and so are points W,Z,O,A, and B.
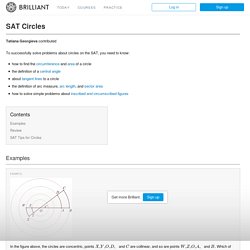
Which of the following has the greatest value? (A) mWX (B) mAD (C) mBC (D) 2mZY (E) It cannot be determined from the information given. Correct Answer: D Solution: Tip: The measure of an arc equals the measure of its central angle. ∠COB≅∠XOW because they are vertical angles. Therefore, m∠COB=m∠DOA=m∠XOW=m∠YOZ=x. High school geometry. Munching on Inscribed Angles. (Restricting the question a little bit, is it true that, in a triangle ABC, the points B, C, Hb, and Hc lie on the same circle?)
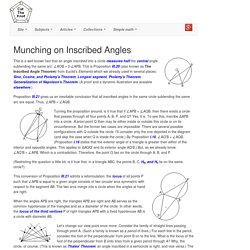
When the angles APB are right, the triangles APB are right and AB serves as the common hypotenuse of the triangles and as a diameter of the circle. In other words, the locus of the third vertices P of right triangles APB with a fixed hypotenuse AB is a circle with diameter AB. Let's change our view point once more. Consider the family of straight lines passing through point A. (Such a family is known as a pencil of lines.) One way to visualize a pencil of lines is to think of a single line that rotates around a fixed center.
We get the following interpretation. We can use the above diagram to make an observation concerning cyclic quadrilaterals: in a convex quadrilateral ABPQ the opposite sides add up to 180°. Angles in Circle |Contact||Front page||Contents||Geometry| As8dspark. By David S.

Park The Central Angle Theorem is very useful in solving questions that deals with angles within circles. The use of this theorem often simplifies a complicated situation into a rather simple one. The Central Angle Theorem is 'central' to many geometric questions involving circles in EMAT 6600, and is highly recommended (by me ^ ^;) to be looked into. Theorem: Central Angle Theorem. Circles. Conjectures in Geometry: Inscribed Angles. Explanation: An inscribed angle is an angle formed by two chords in a circle which have a common endpoint.

Day 4 – Inscribed Angles. Day 4 Inscribed Angles ACTIVITY: Investigating Inscribed Angles Question: An angle in a circle is an inscribed angle if its vertex is on the circle and its sides contain chords of the circle.

How is the measure of an inscribed angle related to the measure of the corresponding central angle? Review of Circle Theorems. This page in the problem solving web site is here primarily as a reminder of some of the usual definitions and theorems pertaining to circles, chords, secants, and tangents.

Some of the entries below could be examined as problems to prove. Mainly, however, these are results we often use in solving other problems. 0. Definition: The measure of an arc of a circle is equal to the measure of the central angle that intercepts the arc. 1. 2. 3.