

Des jeux pour faire des maths. Primaire : Enseigner la résolution de problèmes. M@ths en-vie - Semaine des mathématiques 2019 "Jouons ensemble aux mathématiques". Spip. Continuer à former et à se former en mathématiques : fractions et décimaux Permettre aux élèves d’accéder à des concepts et à leurs représentations en manipulant des objets du quotidien.
Tel est l’objectif visé par les différentes situations et ressources proposées dans cet article. Elles ont été élaborées par un groupe composé de membres de l’IREM de Lille (Institut de Recherche sur l’Enseignement des Mathématiques), des IEN en charge de la Mission Mathématiques et de conseillers pédagogiques. Les ressources proposées s’inscrivent dans la continuité du Plan national et académique Mathématique. Leçon interactive sur les solides. Voici la dernière leçon à manipuler de l’année.
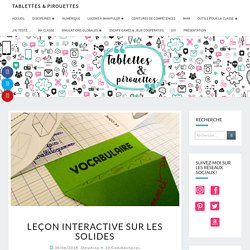
Une leçon qui aura été mise en place sur plusieurs séances, car on l’a complétée au fur et à mesure de nos découvertes (vocabulaire, puis propriétés des solides, puis patrons). C’est une leçon adaptée de la trace écrite proposée dans la Méthode Heuristique de Mathématiques CM1. Au préalable, les élèves avaient pu construire des solides en spaghettis et pâte à modeler, une séance très appréciée de tous et qui fait sens pour le vocabulaire et les propriétés des solides. J’ai récemment expliqué mon fonctionnement avec ce type de leçon, ça n’est pas juste du découpage/collage. Voici quelques propositions réalisées par les élèves lors de la 1ère phase : Comment agencer les différents éléments de la leçon ? Autres configurations. Rémi Brissiaud : Le rapport Villani-Torossian : Analyse de ses choix didactiques. La lettre de mission reçue par les rédacteurs du rapport Villani-Torossian les invitait à « adopter un regard moins théorique et plus opérationnel que les études précédentes ».
Cependant, les deux méthodes mises en avant par le rapport étant l’œuvre de membres de la commission, il était difficile de préconiser leur expérimentation à grande échelle sans un minimum de justifications théoriques. C’est pourquoi on lit dans le rapport que ces méthodes, la Traduction Française de la Méthode de Singapour (TFMS) et celle éditée par le Groupe de Réflexion Interdisciplinaire sur les Programmes (GRIP) ont été retenues parce qu’elles seraient « explicites et intuitives » (page 21). Faire des maths autrement. Au travers des Ateliers de Compréhension de Problèmes (ACP), Roma fournit : - des fiches élèves de situations problèmes - des fiches enseignant explicitant les objectifs des fiches élèves et leur mise en œuvre - une progression structurée de l’apprentissage de la résolution de problèmes sur l’année et sur l’ensemble des cycles 2 et 3.
Au travers des Activités d’Entrainement Individualisé (AEI), Roma fournit : - un découpage des programmes en compétences - pour chaque compétence, une évaluation de chaque élève (numérisée ou sur papier) - après chaque évaluation, selon les résultats obtenus par chacun, un parcours individualisé de 15 activités d’entrainement différenciées. Arithmétique et Compréhension à l’Ecole élémentaire. Un mémo porte-clés en mathématiques pour le CE2. Mathématiques en Éducation prioritaire, des ressources pour la formation.
Défi calcul mental au CP : programmation et générateur. Une année, j’avais créé des générateurs de tests de calcul mental pour le CM1.
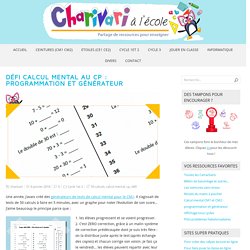
Il s’agissait de tests de 50 calculs à faire en 5 minutes, avec un graphe pour noter l’évolution de son score… J’aime beaucoup le principe parce que : Multi Rapido - jeu Dobble des multiplications. Dernier trimestre de CE2, il est temps de passer à la phase où les tables de multiplications doivent être connues par cœur.
Seulement, il n’est pas envisageable pour moi de me contenter de donner leur apprentissage à faire à la maison. C’est que, malheureusement, là où je travaille, le travail personnel est tout particulièrement incertain et variable d’un enfant à l’autre. De ce fait, je suis bien obligée d’y accorder aussi du temps à l’école. Ça tombe bien puisque, une fois par semaine, nous avons une session dédiée aux jeux en mathématiques afin d’entrainement, principalement, le calcul mental. BATIR : sommaire, mini-leçons, affichages - Le coffre de crapi, zil. Tout à commencer par un livre anglais qui parlait de centres mathématiques et à propos du quel j'ai fait un 1er article : Ensuite nous avons cherché un nom pour adapter le concept au français : Vous pouvez remercier Mecarson sans qui rien ne serait allé aussi vite !
C'est grâce à ses nouveaux commentaires que l'on a tranché sur BATIR (cf cet article) pour le travail mathématique basé sur ce livre (en français !!) J'ai refait la rubrique BATIR et j'ai souhaité gardé la trame de ma/notre réflexion; c'est pourquoi je vous mets les articles du blog en lien. Doc utiles. Math talk cards. M@ths en-vie - Comprendre des concepts mathématiques grâce aux LEGO. Une pratique enseignante Professeure de mathématiques pour les 3ème année dans une école de l’Etat de New York, Alycia Zimmerman a eu l’ingénieuse idée d’utiliser les fameuses briques pour expliquer à ses élèves certains concepts mathématiques.
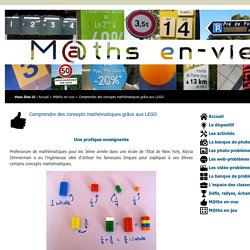
Des legos pour enseigner les mathématiques : cliquer ici Using LEGO to Build Math Concepts : cliquer ici Une séquence complète sur les fractions Objectifs Comprendre et utiliser la notion de fractions simples. Mes 88 ressources élèves en Mathématiques pédagogiquement incontournables. Quelques trouvailles...à ne pas manquer !
Sequence activites debranchees gobelets. Schools and further education. Mathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative Teaching - Jo Boaler, Carol Dweck. There is much concern over the fact that U.S. students perform so poorly in math compared to students in other countries.
Scores of students hate and fear math, students leave school lacking a comprehension of basic mathematical concepts, and the numbers of students choosing math at the college level are in sharp decline. Much of this is blamed on the fact that students just don’t like the subject. Mathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative Teaching (Wiley, Jossey-Bass, 978-0-470-89452-1, November 2015, US $19.95)addresses this issue by giving practical advice and activities for teachers and parents that is all grounded in the latest research. Until now, research on mathematics learning and the brain has been communicated through research journals. New brain research on Mathematics LearningThe Power of Mistakes and StruggleWhat Is Math Really?
Home - YouCubed. Ceintures de Mesures (CM1-CM2) – Charivari à l'école. Dans mes classes, convertir, comparer, additionner ou soustraire des mesures exprimées dans des unités différentes, c’est toujours compliqué et, sans ceintures, je n’arrivais pas à « emmener tout le monde ».

Voilà trois ans que j’y pense mais que je ne trouve pas le temps de les formaliser. Ces ceintures de mesure étaient presque prêtes dans ma tête, j’avais déjà préparé et fait essayer pas mal de choses à mes élèves… mais il me restait à les produire. Je fonde donc beaucoup d’espoir sur ces nouvelles ceintures. Vous verrez que, pour la première fois, j’ai adopté le QCM. Je me suis inspirée des manuels Sesamaths, que mon fils a utilisés au collège, et qui en proposent dans tous leur chapitres. Loïc Rouault : Appréhender le codage en technologie. Comment aborder le codage en 6ème sans ordinateur ? Comment mettre en place un projet pluridisciplinaire avec Scratch ? Loïc Rouault, enseignant de technologie au collège Sainte Croix de Châteaugiron (35) et formateur numérique revient sur les nouveaux programmes de technologie au collège. Loïc Rouault nous livre son approche du codage avec ses élèves. « L’idée est de rendre l’élève actif et partie prenante de projets où la plus-value pédagogique est importante ».
Après 30 ans de carrière, l’enseignant revient aussi sur la dématérialisation continue de l’enseignement de la technologie. Un nouveau tome de 1, 2, 3 codez ! Initiation Scratch junior. Avant le grand départ en vacances, piquez la curiosité de vos élèves de primaire ! Chloé Rutigliano, professeure des écoles dans le Marne, invite les plus jeunes à faire un grand parcours de découvertes : on commence avec une initiation au code sur le logiciel Scratch, en faisant un arrêt à la ferme pour apprendre les animaux en anglais, et enfin avec une activité pour apprendre ou réviser le calcul des distances en kilomètres ou mètres.
Un itinéraire qui attirera tous les audacieux et les aventuriers ! Vous avez peut-être déjà entendu parler de Scratch, un langage de programmation simplifié destiné aux enfants de 8 à 16 ans ? Scratch est utilisé par des milliers d’enfants et d’adultes dans le monde. L’utilisation de Scratch se fait en ligne, gratuitement et en Français avec, entre autres, des forums francophones. Passez ensuite à une activité destinée à vous faire apprendre de manière ludique les différents animaux de la ferme en anglais. Mathématique… vers une méthode naturelle : un exemple de pratique au cycle 3 par Sylvain Hannebique – Ch'ti qui.
Christophe Auclair : Des applications mathématiques pour le collège. Vous connaissez beaucoup d'académies qui éditent elles-mêmes des applications pédagogiques ? L'académie de Dijon le fait grâce à Christophe Auclair, un professeur de maths déchargé à mi temps. Dans quelques jours il publiera sa 7ème application de l'année pour le collège. Une vocation gagnée en Rep au service des élèves. Etre utile aux élèves. Colloque Mathématiques en Cycle 3, 8-9 juin 2017, Poitiers.