

Dimensional analysis. Dimensional analysis is routinely used as a check on the plausibility of derived equations and computations.
It is also used to categorize types of physical quantities and units based on their relationship to or dependence on other units. Great principle of similitude[edit] The basic principle of dimensional analysis was known to Isaac Newton (1686) who referred to it as the "Great Principle of Similitude".[1] James Clerk Maxwell played a major role in establishing modern use of dimensional analysis by distinguishing mass, length, and time as fundamental units, while referring to other units as derived.[2] The 19th-century French mathematician Joseph Fourier made important contributions[3] based on the idea that physical laws like F = ma should be independent of the units employed to measure the physical variables.
Definition[edit]
Tesseract. A generalization of the cube to dimensions greater than three is called a "hypercube", "n-cube" or "measure polytope".[1] The tesseract is the four-dimensional hypercube, or 4-cube.
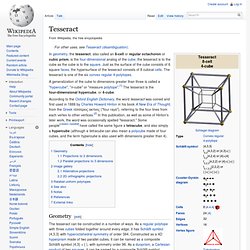
According to the Oxford English Dictionary, the word tesseract was coined and first used in 1888 by Charles Howard Hinton in his book A New Era of Thought, from the Greek τέσσερεις ακτίνες ("four rays"), referring to the four lines from each vertex to other vertices.[2] In this publication, as well as some of Hinton's later work, the word was occasionally spelled "tessaract. " Some people[citation needed] have called the same figure a tetracube, and also simply a hypercube (although a tetracube can also mean a polycube made of four cubes, and the term hypercube is also used with dimensions greater than 4).
Geometry[edit] Dimension (vector space) For every vector space there exists a basis,[b] and all bases of a vector space have equal cardinality;[c] as a result, the dimension of a vector space is uniquely defined.
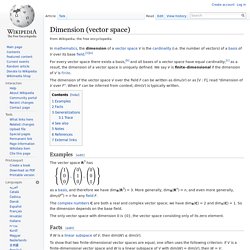
We say V is finite-dimensional if the dimension of V is finite. The dimension of the vector space V over the field F can be written as dimF(V) or as [V : F], read "dimension of V over F". When F can be inferred from context, dim(V) is typically written. The vector space R3 has The complex numbers C are both a real and complex vector space; we have dimR(C) = 2 and dimC(C) = 1. The only vector space with dimension 0 is {0}, the vector space consisting only of its zero element.
If W is a linear subspace of V, then dim(W) ≤ dim(V). To show that two finite-dimensional vector spaces are equal, one often uses the following criterion: if V is a finite-dimensional vector space and W is a linear subspace of V with dim(W) = dim(V), then W = V. Any two vector spaces over F having the same dimension are isomorphic. Manifolds. Dimension of an algebraic variety. In mathematics and specifically in algebraic geometry, the dimension of an algebraic variety may be defined in various equivalent ways.
Some of these definitions are of geometric nature, while some other are purely algebraic and rely on commutative algebra. Some are restricted to algebraic varieties while others apply also to any algebraic set. Some are intrinsic, as independent of any embedding of the variety into an affine or projective space, while other are related to such an embedding. Krull dimension. The Krull dimension has been introduced to provide an algebraic definition of the dimension of an algebraic variety: the dimension of the affine variety defined by an ideal I in a polynomial ring R is the Krull dimension of R/I.

A field k has Krull dimension 0; more generally, k[x1, ..., xn] has Krull dimension n. A principal ideal domain that is not a field has Krull dimension 1. A local ring has Krull dimension 0 if and only if every element of its maximal ideal is nilpotent. Explanation[edit] Inductive dimension. The small and large inductive dimensions are two of the three most usual ways of capturing the notion of "dimension" for a topological space, in a way that depends only on the topology (and not, say, on the properties of a metric space).
The other is the Lebesgue covering dimension. The term "topological dimension" is ordinarily understood to refer to Lebesgue covering dimension. For "sufficiently nice" spaces, the three measures of dimension are equal. Formal definition[edit] We want the dimension of a point to be 0, and a point has empty boundary, so we start with Then inductively, ind(X) is the smallest n such that, for every. Lebesgue covering dimension. In mathematics, the Lebesgue covering dimension or topological dimension of a topological space is one of several different ways of defining the dimension of the space in a topologically invariant way.
Definition[edit] As a special case, a topological space is zero-dimensional with respect to the covering dimension if every open cover of the space has a refinement consisting of disjoint open sets so that any point in the space is contained in exactly one open set of this refinement. Examples[edit] More generally, the n-dimensional Euclidean space has covering dimension n.
A non-technical illustration of these examples below. Properties[edit] Hausdorff dimension. In mathematics, the Hausdorff dimension (also known as the Hausdorff–Besicovitch dimension) is an extended non-negative real number associated with any metric space.
Gilbert spaces.