

A surface such as a plane or the surface of a cylinder or sphere has a dimension of two because two coordinates are needed to specify a point on it – for example, both a latitude and longitude is required to locate a point on the surface of a sphere. The inside of a cube, a cylinder or a sphere is three-dimensional because three coordinates are needed to locate a point within these spaces.
In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that was found necessary to describe electromagnetism. The four dimensions of spacetime consists of events that are not absolutely defined spatially and temporally, but rather are known relative to the motion of an observer. Minkowski space first approximates the universe without gravity; the pseudo-Riemannian manifolds of general relativity describe spacetime with matter and gravity. Ten dimensions are used to describe string theory, and the state-space of quantum mechanics is an infinite-dimensional function space.
The concept of dimension is not restricted to physical objects. High-dimensional spaces frequently occur in mathematics and the sciences. They may be parameter spaces or configuration spaces such as in Lagrangian or Hamiltonian mechanics; these are abstract spaces, independent of the physical space we live in.
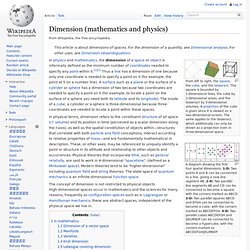
Dimension. A diagram showing the first four spatial dimensions. 1-D: Two points A and B can be connected to a line, giving a new line segment AB. 2-D: Two parallel line segments AB and CD can be connected to become a square, with the corners marked as ABCD. 3-D: Two parallel squares ABCD and EFGH can be connected to become a cube, with the corners marked as ABCDEFGH. 4-D: Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to become a hypercube, with the corners marked as ABCDEFGHIJKLMNOP.
In physical terms, dimension refers to the constituent structure of all space (cf. volume) and its position in time (perceived as a scalar dimension along the t-axis), as well as the spatial constitution of objects within—structures that correlate with both particle and field conceptions, interact according to relative properties of mass—and are fundamentally mathematical in description. The concept of dimension is not restricted to physical objects. A tesseract is an example of a four-dimensional object.
Dimensions in Physics. Networks and dimension. Fourth dimension in literature. The idea of a fourth dimension has been a factor in the evolution of modern art, but use of concepts relating to higher dimensions has been little discussed by academics in the literary world.[1] From the late 1800s onwards, many writers began to make use of possibilities opened up by the exploration of such concepts as hypercubes and non-Euclidian geometry.
While many writers took the fourth dimension to be one of time (as it is commonly considered today), others preferred to think of it in spatial terms, and some associated the new mathematics with wider changes in modern culture. Early influence[edit] Dimensions in Philosophy.
One dimensional topics. Two dimensional topics. Three dimensional topics. Four dimensional topics. Infinite dimensional topics. .bodycard 2266.