

Split-quaternion. Ij = k = −ji, jk = −i = −kj, ki = j = −ik, i2 = −1, j2 = +1, k2 = +1, and hence ijk = 1.
A coquaternion q = w + xi + yj + zk, has a conjugate q* = w − xi − yj − zk, and multiplicative modulus qq* = w2 + x2 − y2 − z2. This quadratic form is split into positive and negative parts, in contrast to the positive definite form on the algebra of quaternions. When the modulus is non-zero, then q has a multiplicative inverse, namely q*/qq*. The split-quaternion basis can be identified as the basis elements of either the Clifford algebra Cℓ1,1(R), with {1, e1 = i, e2 = j, e1e2 = k}; or the algebra Cℓ2,0(R), with {1, e1 = j, e2 = k, e1e2 = i}. Historically coquaternions preceded Cayley's matrix algebra; coquaternions (along with quaternions and tessarines) evoked the broader linear algebra.
Matrix representations[edit] Let and consider u = w + xi, and v = y + zi as ordinary complex numbers with complex conjugates denoted by u* = w − xi, v* = y − zi. Quaternion group. Where 1 is the identity element and −1 commutes with the other elements of the group.
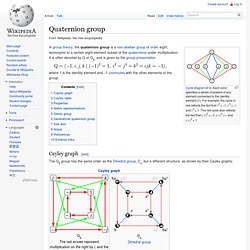
Cayley graph[edit] The Q8 group has the same order as the Dihedral group, D4, but a different structure, as shown by their Cayley graphs: Cayley table[edit] The Cayley table (multiplication table) for Q is given by:[1] The multiplication of pairs of elements from the subset {±i, ±j, ±k} works like the cross product of unit vectors in three-dimensional Euclidean space. Properties[edit] The quaternion group has the unusual property of being Hamiltonian: every subgroup of Q is a normal subgroup, but the group is non-abelian.[2] Every Hamiltonian group contains a copy of Q.[3] In abstract algebra, one can construct a real four-dimensional vector space with basis {1, i, j, k} and turn it into an associative algebra by using the above multiplication table and distributivity.
Qubit. In quantum computing, a qubit/ˈkjuːbɪt/ or quantum bit is a unit of quantum information—the quantum analogue of the classical bit.
A qubit is a two-state quantum-mechanical system, such as the polarization of a single photon: here the two states are vertical polarization and horizontal polarization. In a classical system, a bit would have to be in one state or the other, but quantum mechanics allows the qubit to be in a superposition of both states at the same time, a property which is fundamental to quantum computing. Bit versus qubit[edit] A bit is the basic unit of information. It is used to represent information by computers. Quantum gate. In quantum computing and specifically the quantum circuit model of computation, a quantum gate (or quantum logic gate) is a basic quantum circuit operating on a small number of qubits.
They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits. Unlike many classical logic gates, quantum logic gates are reversible. However, classical computing can be performed using only reversible gates. For example, the reversible Toffoli gate can implement all Boolean functions. This gate has a direct quantum equivalent, showing that quantum circuits can perform all operations performed by classical circuits. Quantum logic gates are represented by unitary matrices. Commonly used gates[edit] Quantum gates are usually represented as matrices. Hadamard gate[edit] The Hadamard gate acts on a single qubit. To and and represents a rotation of about the axis . Circuit representation of Hadamard gate Since Pauli-X gate[edit] . Reversible computing. Reversible computing is a model of computing where the computational process to some extent is reversible, i.e., time-invertible.
In a computational model that uses transitions from one state of the abstract machine to another, a necessary condition for reversibility is that the relation of the mapping from states to their successors must be one-to-one. Reversible computing is generally considered an unconventional form of computing. There are two major, closely related, types of reversibility that are of particular interest for this purpose: physical reversibility and logical reversibility.[1] A process is said to be physically reversible if it results in no increase in physical entropy; it is isentropic.
These circuits are also referred to as charge recovery logic, adiabatic circuits, or adiabatic computing. As was first argued by Rolf Landauer of IBM,[3] in order for a computational process to be physically reversible, it must also be logically reversible. Reversible circuits[edit] . Quadratic programming. Quadratic programming (QP) is a special type of mathematical optimization problem.
It is the problem of optimizing (minimizing or maximizing) a quadratic function of several variables subject to linear constraints on these variables. Problem formulation[edit] The quadratic programming problem can be formulated as:[1] Assume x belongs to Minimize (with respect to x) Subject to one or more constraints of the form: (inequality constraint) (equality constraint) where indicates the vector transpose of . Means that every entry of the vector is less than or equal to the corresponding entry of the vector.