

Systems Theory/Cybernetics. What is Cybernetics?
[edit] Data Structures. This book is about the creation and analysis of efficient data structures.
It covers: the primitive node structure;asymptotic notation for mathematically discussing performance characteristics;built-in arrays;list structures built from either nodes or arrays;iterators as an abstract model of enumerating the items in a sequence;stacks and queues for computing with last-in/first-out and first-in/first-out orderings;binary and general tree structures for searching or representing hierarchical relationships;min and max heaps for representing ordering based on priorities;graph structures for representing more general relationships between data elements;hash tables for the efficient retrieval of strings and other objects; and finallytrade-offs between the structures, and strategies for picking the most appropriate ones.
Because many different languages approach the construction of data structures differently, we use pseudo-code so that you can translate the code into your own language. Algorithms. Preamble[edit] This book aims to be an accessible introduction into the design and analysis of efficient algorithms.
Throughout the book we will introduce only the most basic techniques and describe the rigorous mathematical methods needed to analyze them. The topics covered include: The divide and conquer technique.The use of randomization in algorithms.The general, but typically inefficient, backtracking technique.Dynamic programming as an efficient optimization for some backtracking algorithms.Greedy algorithms as an optimization of other kinds of backtracking algorithms.Hill-climbing techniques, including network flow. The goal of the book is to show you how you can methodically apply different techniques to your own algorithms to make them more efficient. List of concurrent and parallel programming languages. The following categories aim to capture the main, defining feature of the languages contained, but they are not necessarily orthogonal.
Actor model[edit] Coordination languages[edit] List of concurrent and parallel programming languages. Quora - Un lieu pour partager le savoir et mieux comprendre le monde. Language of mathematics. Outline of discrete mathematics. Included below are many of the standard terms used routinely in university-level courses and in research papers.
This is not, however, intended as a complete list of mathematical terms; just a selection of typical terms of art that may be encountered. Subjects in discrete mathematics[edit] Discrete mathematical disciplines[edit] For further reading in discrete mathematics, beyond a basic level, see these pages. Many of these disciplines are closely related to computer science.
LMSection1p1. Why the Arabic World Turned Away from Science. Hillel Ofek Contemporary Islam is not known for its engagement in the modern scientific project.
But it is heir to a legendary “Golden Age” of Arabic science frequently invoked by commentators hoping to make Muslims and Westerners more respectful and understanding of each other. President Obama, for instance, in his June 4, 2009 speech in Cairo, praised Muslims for their historical scientific and intellectual contributions to civilization: It was Islam that carried the light of learning through so many centuries, paving the way for Europe’s Renaissance and Enlightenment. Polynomials. A polynomial looks like this: Polynomial comes from poly- (meaning "many") and -nomial (in this case meaning "term") ... so it says "many terms" A polynomial can have:

Quora - Un lieu pour partager le savoir et mieux comprendre le monde. InTech Process capability and six sigma methodology including fuzzy and lean approaches. SixSigma. Amazon. Mathematics as Language. Summation Notation. Often mathematical formulae require the addition of many variables Summation or sigma notation is a convenient and simple form of shorthand used to give a concise expression for a sum of the values of a variable.

Let x1, x2, x3, …xn denote a set of n numbers. x1 is the first number in the set. xi represents the ith number in the set. Summation notation involves: The summation sign This appears as the symbol, S, which is the Greek upper case letter, S. The summation sign, S, instructs us to sum the elements of a sequence. A typical element of the sequence which is being summed appears to the right of the summation sign.
The variable of summation, i.e. the variable which is being summed The variable of summation is represented by an index which is placed beneath the summation sign. What is Sigma? - Definition & Concept. What is Sigma? - Definition & Concept. Online maths practice. Kerckhoffs's principle. In cryptography, Kerckhoffs's principle (also called Kerckhoffs's desiderata, Kerckhoffs's assumption, axiom, or law) was stated by Auguste Kerckhoffs in the 19th century: A cryptosystem should be secure even if everything about the system, except the key, is public knowledge.
Origins[edit] In 1883 Auguste Kerckhoffs[1] wrote two journal articles on La Cryptographie Militaire,[2] in which he stated six design principles for military ciphers. Translated from French, they are:[3] Some are no longer relevant given the ability of computers to perform complex encryption, but his second axiom, now known as Kerckhoffs's principle, is still critically important. MATHEMATICS & RELATED ANIMATIONS. Statistical learning. R. From Wolfram MathWorld. A matrix is a concise and useful way of uniquely representing and working with linear transformations.
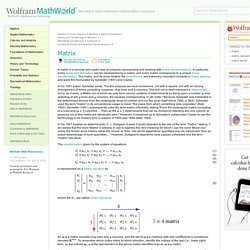
In particular, every linear transformation can be represented by a matrix, and every matrix corresponds to a unique linear transformation. The matrix, and its close relative the determinant, are extremely important concepts in linear algebra, and were first formulated by Sylvester (1851) and Cayley. In his 1851 paper, Sylvester wrote, "For this purpose we must commence, not with a square, but with an oblong arrangement of terms consisting, suppose, of lines and columns. R-Language Tools. R-How2s. Response Surface Methodology.