

Fuzzy cognitive map. A collection of papers with applications in various disciplines is presented in the book "Fuzzy Cognitive Maps: Advances in Theory, Methodologies, Applications and Tools[5] edited by Michael Glykas and prefaced by Bart Kosko.
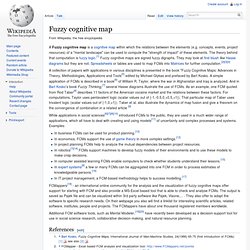
A simple application of FCMs is described in a book[6] of William R. Taylor, where the war in Afghanistan and Iraq is analyzed. And in Bart Kosko's book Fuzzy Thinking,[7] several Hasse diagrams illustrate the use of FCMs. As an example, one FCM quoted from Rod Taber[8] describes 11 factors of the American cocaine market and the relations between these factors. For computations, Taylor uses pentavalent logic (scalar values out of {-1,-0.5,0,+0.5,+1}). While applications in social sciences[6][7][8][10] introduced FCMs to the public, they are used in a much wider range of applications, which all have to deal with creating and using models[11] of uncertainty and complex processes and systems.
FCMapper - our Fuzzy Cognitive Mapping Software Solution. Cognitive map. Overview[edit] Cognitive maps serve the construction and accumulation of spatial knowledge, allowing the "mind's eye" to visualize images in order to reduce cognitive load, enhance recall and learning of information.
This type of spatial thinking can also be used as a metaphor for non-spatial tasks, where people performing non-spatial tasks involving memory and imaging use spatial knowledge to aid in processing the task.[6] The neural correlates of a cognitive map have been speculated to be the place cell system in the hippocampus[7] and the recently discovered grid cells in the entorhinal cortex.[8] Neurological basis[edit] Cognitive mapping is believed to largely be a function of the hippocampus. Numerous studies by O'Keefe have implicated the involvement of place cells. Parallel map theory[edit] Generation[edit] The cognitive map is generated from a number of sources, both from the visual system and elsewhere.
History[edit] The idea of a cognitive map was first developed by Edward C. FUZZY LOGIC FOR BUSINESS, FINANCE, AND MANAGEMENT. Fuzzy Logic in Finance. Fuzzy associative matrix. A fuzzy associative matrix expresses fuzzy logic rules in tabular form.
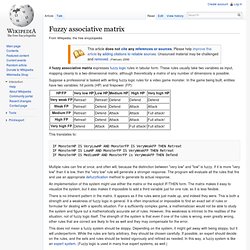
These rules usually take two variables as input, mapping cleanly to a two-dimensional matrix, although theoretically a matrix of any number of dimensions is possible. Suppose a professional is tasked with writing fuzzy logic rules for a video game monster. In the game being built, entities have two variables: hit points (HP) and firepower (FP): This translates to: IF MonsterHP IS VeryLowHP AND MonsterFP IS VeryWeakFP THEN Retreat IF MonsterHP IS LowHP AND MonsterFP IS VeryWeakFP THEN Retreat IF MonsterHP IS MediumHP AND MonsterFP is VeryWeakFP THEN Defend Multiple rules can fire at once, and often will, because the distinction between "very low" and "low" is fuzzy.
An implementation of this system might use either the matrix or the explicit IF/THEN form. There is no inherent pattern in the matrix. This does not mean a fuzzy system should be sloppy. Defuzzification. Defuzzification is the process of producing a quantifiable result in fuzzy logic, given fuzzy sets and corresponding membership degrees.
It is typically needed in fuzzy control systems. These will have a number of rules that transform a number of variables into a fuzzy result, that is, the result is described in terms of membership in fuzzy sets. For example, rules designed to decide how much pressure to apply might result in "Decrease Pressure (15%), Maintain Pressure (34%), Increase Pressure (72%)".
Defuzzification is interpreting the membership degrees of the fuzzy sets into a specific decision or real value. The simplest but least useful defuzzification method is to choose the set with the highest membership, in this case, "Increase Pressure" since it has a 72% membership, and ignore the others, and convert this 72% to some number. Fuzzy logic. Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact.
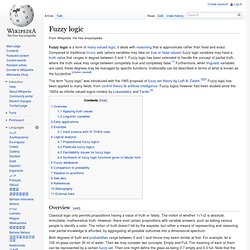
Compared to traditional binary sets (where variables may take on true or false values) fuzzy logic variables may have a truth value that ranges in degree between 0 and 1. Fuzzy logic has been extended to handle the concept of partial truth, where the truth value may range between completely true and completely false.[1] Furthermore, when linguistic variables are used, these degrees may be managed by specific functions. Irrationality can be described in terms of what is known as the fuzzjective. Lotfi A. Zadeh. Lotfali Askar Zadeh (born February 4, 1921), better known as Lotfi A.
Zadeh, is a mathematician, electrical engineer, computer scientist, artificial intelligence researcher and professor emeritus[1] of computer science at the University of California, Berkeley. Life and career[edit] Zadeh was born in Baku, Azerbaijan SSR,[2] as Lotfi Aliaskerzadeh,[3] to an Iranian Azerbaijanis father from Ardabil, Rahim Aleskerzade, who was a journalist on assignment from Iran, and a Russian Jewish mother,[4] Fanya Koriman, who was a pediatrician.[5] The Soviet government at this time courted foreign correspondents, and the family lived well while in Baku.[6] Zadeh attended elementary school for three years there,[6] which he has said "had a significant and long-lasting influence on my thinking and my way of looking at things. "[7] In 1931, when Zadeh was ten years old, his family moved to Tehran in Iran, his father's homeland. Fuzzy set. It has been suggested by Thayer Watkins that Zadeh's ethnicity is an example of a fuzzy set because "His father was Turkish-Iranian (Azerbaijani) and his mother was Russian.
Fuzzy cognitive map. Relational database. In the relational model, each table schema must identify a column or group of columns, called the primary key, to uniquely identify each row.
A relationship can then be established between each row in the table and a row in another table by creating a foreign key, a column or group of columns in one table that points to the primary key of another table. The relational model offers various levels of refinement of table organization and reorganization called database normalization. (See Normalization below.) T-norm fuzzy logics. T-norm fuzzy logics are a family of non-classical logics, informally delimited by having a semantics which takes the real unit interval [0, 1] for the system of truth values and functions called t-norms for permissible interpretations of conjunction.
They are mainly used in applied fuzzy logic and fuzzy set theory as a theoretical basis for approximate reasoning. T-norm fuzzy logics belong in broader classes of fuzzy logics and many-valued logics. In order to generate a well-behaved implication, the t-norms are usually required to be left-continuous; logics of left-continuous t-norms further belong in the class of substructural logics, among which they are marked with the validity of the law of prelinearity, (A → B) ∨ (B → A).