

Math Gems. MathPages. Banach-Tarski Paradox. Did you know that it is possible to cut a solid ball into 5 pieces, and by re-assembling them, using rigid motions only, form TWO solid balls, EACH THE SAME SIZE AND SHAPE as the original?

This theorem is known as the Banach-Tarski paradox. So why can't you do this in real life, say, with a block of gold? If matter were infinitely divisible (which it is not) then it might be possible. But the pieces involved are so "jagged" and exotic that they do not have a well-defined notion of volume, or measure, associated to them.
In fact, what the Banach-Tarski paradox shows is that no matter how you try to define "volume" so that it corresponds with our usual definition for nice sets, there will always be "bad" sets for which it is impossible to define a "volume"! Presentation Suggestions: Students will find this Fun Fact hard to believe. The Math Behind the Fact: First of all, if we didn't restrict ourselves to rigid motions, this paradox would be more believable. Khan Academy. Integral Table. Take It to the Limit. In middle school my friends and I enjoyed chewing on the classic conundrums.
What happens when an irresistible force meets an immovable object? Easy — they both explode. Philosophy’s trivial when you’re 13. But one puzzle bothered us: if you keep moving halfway to the wall, will you ever get there? Something about this one was deeply frustrating, the thought of getting closer and closer and yet never quite making it. Questions like this have always caused headaches. But Archimedes, the greatest mathematician of antiquity, realized the power of the infinite. In the coming weeks we’ll delve into the great ideas at the heart of calculus.
If you’re a careful thinker, you might be worried about something already. Imagine using a photocopier to reduce an image of a circle by, say, 50 percent. Of course, this doesn’t tell us how big pi is. Before turning to Archimedes’s brilliant solution, we should mention one other place where pi appears in connection with circles. Yes, it is. Calculus Mega Cheat Sheet.
Prehistoric Calculus: Discovering Pi. Pi is mysterious.
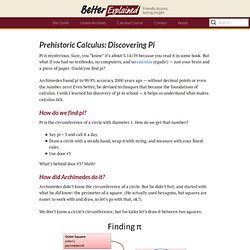
Sure, you “know” it’s about 3.14159 because you read it in some book. But what if you had no textbooks, no computers, and no calculus (egads!) — just your brain and a piece of paper. Could you find pi? Archimedes found pi to 99.9% accuracy 2000 years ago — without decimal points or even the number zero! How do we find pi? Pi is the circumference of a circle with diameter 1. Say pi = 3 and call it a day.Draw a circle with a steady hand, wrap it with string, and measure with your finest ruler.Use door #3 What’s behind door #3?
How did Archimedes do it? Archimedes didn’t know the circumference of a circle. We don’t know a circle’s circumference, but for kicks let’s draw it between two squares: Neat — it’s like a racetrack with inner and outer edges. And since squares are, well, square, we find their perimeters easily: Outside square (easy): side = 1, therefore perimeter = 4Inside square (not so easy): The diagonal is 1 (top-to-bottom). Squares drool, octagons rule Cool! Free Calculus. The Calculus Here is a free online calculus course.

This is essentially an ordinary text, but you can read it online. There are lots of exercises and examples. As we get the chapters scanned in, they will become highlighted so that you can click on them to read. This text is somewhat unusual for two reasons. The text is rigorous. Both points are no doubt controversial, but conceptually the approach gives a kind of clean synergy which generates important examples and unifies calculus to a great extent. Unfortunately, there are no doubt uncorrected typographical errors and logical errors. MathPages.