

Dart%20Board%20-%20multiplication. F%20D%20P%20balance%20v7. MyMaths - Bringing Maths Alive. Blockbuster%20v4. Skillswise - Homepage. Wiris.com. Download. Mathematiques et sciences physiques avec Geogebra(Daniel Mentrard) Plein de documents, d'applets, d'activités pour la maternelle, l'école primaire, le collège, le lycée et l'université avec ou sans GeoGebra ; des exercices, des animations, des simulations pour les Mathématiques et les Sciences physiques pour tous les niveaux d'enseignement.

Vous êtes nombreux à vouloir vous servir mais comme il n'y a pratiquement pas de liens retour vers ce site* ....... A ce jour ,il y a environ 8000 fichiers Geogebra dont beaucoup sont déja recopiés sur de nombreux sites ou livres sans même citer leur origine et sans autorisation de l'auteur . Magnifique !! Je rappelle à tous que ces fichiers mis gratuitement en ligne ne me rapportent rien contrairement à ce que certains pensent .Mais ,peut- être ,ai-je tort ? Teacher Portal - Sumdog's free maths games. Sumdog > Sumdog's features > Games Sumdog's maths games are all free to play, whether you're at home or in school.

(Why are they free?). Most of Sumdog's games are multiplayer - which means you can choose to play against other Sumdog users around the world. Although the games are all different, they all have one thing in common: you need to answer maths questions to make progress. VocabGrabber. Math problems + puzzle for kids. The odd genius who showed that one infinity was greater than another. A mathematical bug shows us why the 3D universe leads to Murphy's Law. Let's also not forget that unlike, a path, the movement of any string no matter how thin is at least partially governed by the slight recoiling that occurs at the bends and curves.
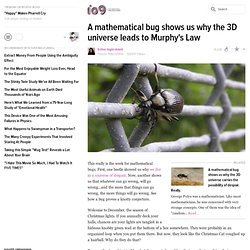
I think analogies are wonderful for explaining complex systems to simple folk like myself, but I hate it when "scientists" try to prove a mathematical system with an insufficient metaphor. Exactly what I was thinking. The way a string falls is not random. Even if you stood there shaking the box it still has all manner of constraints based on where parts of the string both forward and backward from each position are. A mathematical bug shows us why the 3D universe carries the possibility of despair. Really. For N bug-steps, there are two things to consider: how many total possible paths of N steps the bug has available to it, and how many of those N-step paths lead home.

The simplest proof mathematicians needed two tries at. What are Amicable Numbers? Four color theorem. Example of a four-colored map A four-coloring of a map of the states of the United States (ignoring lakes).
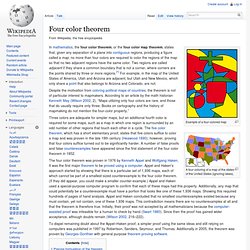
In mathematics, the four color theorem, or the four color map theorem, states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. Bifurcation diagram. In mathematics, particularly in dynamical systems, a bifurcation diagram shows the possible long-term values (equilibria/fixed points or periodic orbits) of a system as a function of a bifurcation parameter in the system.
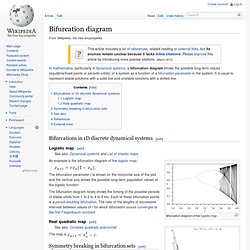
It is usual to represent stable solutions with a solid line and unstable solutions with a dotted line. Bifurcations in 1D discrete dynamical systems[edit] Logistic map[edit] Animation showing the formation of bifurcation diagram An example is the bifurcation diagram of the logistic map: The bifurcation parameter r is shown on the horizontal axis of the plot and the vertical axis shows the possible long-term population values of the logistic function.
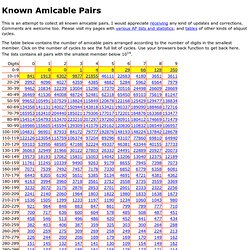
The bifurcation diagram nicely shows the forking of the possible periods of stable orbits from 1 to 2 to 4 to 8 etc. Real quadratic map[edit] The map is Symmetry breaking in bifurcation sets[edit] Known Amicable Pairs. This is an attempt to collect all known amicable pairs.
The Amazing Mathematics of Nov. 11, 2011. Today's date, 11/11/11, is a once-in-a-century occurrence, adding to a November has been a very fun month for recreational mathematicians.

Uncovering Da Vinci's Rule of the Trees. As trees shed their foliage this fall, they reveal a mysterious, nearly universal growth pattern first observed by Leonardo da Vinci 500 years ago: a simple yet startling relationship that always holds between the size of a tree's trunk and sizes of its branches.

The nature of nothingness. Zilch… Naught… Nada… It’s easy to dismiss the concept of nothing as, well, nothing.
In fact, nothing is everything to science – understanding the intangible voids has lead to breakthroughs we could never have imagined possible. Read on to find out why nothing is more important than nothing… Nothingness: Zero, the number they tried to ban Every schoolchild knows the concept of zero – so why did it take so long to catch on? Follow its convoluted path from heresy to common sense. Los socorridos números de Fibonacci. La secuencia de Fibonacci es una sucesión infinita de números naturales. Se denominan así los números que permiten contar los elementos de un conjunto. Son el primer grupo de números que fueron usados por los seres humanos para contar cosas. El uno, el dos, el cinco, por nombrar algunos, son números naturales. En la secuencia de Fibonacci cada número viene dado por la suma de los dos anteriores.
How To: 1 x 8 1=9 - Beauty of Mathematics. Math in a Minute: Welcome to Hotel Infinity paradox. Mathematics as the raw material for art. Kat Austen, Culture Lab editor (Image: Hiroshi Sugimoto) In a new Paris exhibition, prizewinning mathematicians team up with artists to inspire works that bring intangible concepts to life Mathematics - A Beautiful Elsewhere, Fondation Cartier, Paris, until 18 March IF YOU think of cosmology, you picture colourful nebulae; with neurology, intricate brain scans.
But what does mathematics look like? The product of the collaboration is the exhibition Mathematics - A Beautiful Elsewhere, at the Fondation Cartier in Paris, France. Ambitious perhaps, but the team has impressive credentials: the mathematical line-up boasts three Fields medal winners, including 2010 recipient Cédric Villani. Canal de Vihart. The Coastline Paradox & The Koch Snowflake. How do japanese multiply?? The Fibonacci Sequence.