Les théorèmes de Gödel : fin d’un espoir ? - Université de Bordeaux - SAM. L'énigme des quipus incas enfin élucidée ? COMMUNICATION.
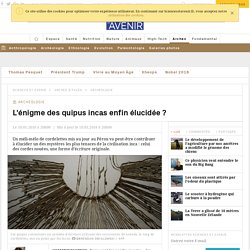
Rares sont les cordes nouées – les quipus (nœud, en langue quechua) – parvenues jusqu’à nous. La découverte de vingt-neuf d’entre elles sur le site d’Incahuasi dans la vallée de Canete, à 160 km sud de Lima au Pérou, constitue donc un événement archéologique exceptionnel comme l’a expliqué au New York Times Gary Urton, l’un des principaux spécialistes des quipus : "Elles ont été retrouvées dans un entrepôt de stockage de produits agricoles (…) de cette cité bâtie au 15e siècle.
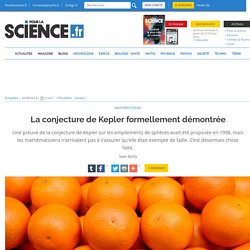
" La conjecture de Kepler formellement démontrée. Quelle est la meilleure façon d'empiler les oranges, les pommes ou les melons sur les étalages des primeurs pour perdre le moins d'espace possible ?
There’s one key difference between kids who excel at math and those who don’t — Quartz. “I’m just not a math person.”
We hear it all the time. And we’ve had enough. Because we believe that the idea of “math people” is the most self-destructive idea in America today. The truth is, you probably are a math person, and by thinking otherwise, you are possibly hamstringing your own career. Worse, you may be helping to perpetuate a pernicious myth that is harming underprivileged children—the myth of inborn genetic math ability. Is math ability genetic? How do we know this? Different kids with different levels of preparation come into a math class. Reflexions de J-F Colonna - Images des mathématiques. Les Mathématiques existent-elles en dehors de l’esprit des mathématiciens et donc indépendamment de nous ?
Et si oui, leur redoutable efficacité en Physique ne serait-elle pas le signe que notre Réalité est une structure mathématique ? Les progrès en Mathématiques dites pures se font en général grâce à des problèmes posés, tels des défis, à la communauté des mathématiciens par l’un de ses membres [1]. La plupart du temps, pour ne pas dire toujours, ces questions sont abstraites, souvent incompréhensibles pour le commun des mortels et sans rapport apparent avec la Réalité tangible.
Un exemple récent, qui fit la une des journaux, fut la démonstration du Grand Théorème de Fermat par Andrew Wiles après plus de trois siècles de tâtonnements, d’erreurs et d’efforts. GeoGebra. Images des mathématiques. Bienvenue sur ChronoMath, une chronologie des mathématiques.
Ondelette. Un article de Wikipédia, l'encyclopédie libre.
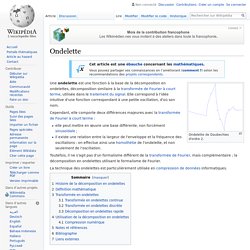
Ondelette de Daubechies d'ordre 2. Triangle de Reuleaux. Un article de Wikipédia, l'encyclopédie libre.
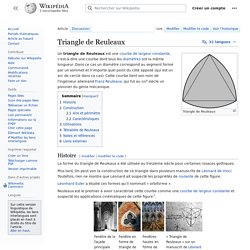
Un triangle de Reuleaux est une courbe de largeur constante, c'est-à-dire une courbe dont tous les diamètres ont la même longueur. Dans ce cas un diamètre correspond au segment formé par un sommet et n'importe quel point du côté opposé (qui est un arc de cercle dans ce cas). Cette courbe tient son nom de l'ingénieur allemand Franz Reuleaux, qui fut au XIXe siècle un pionnier du génie mécanique. Troll pi explained @ Things Of Interest. Here's the "Troll Pi" or "Pi equals 4" image.

Here's the breakdown, as simple as I can make it. All of the following facts are true: Panels one to four describe a sequence of curves. (Here, "curve" is a generic term referring to any continuous line, be it straight or crooked or curved.)Each curve in the sequence has a well-defined length of exactly 4. These facts are also true: The sequence of curves converges uniformly on a limit.As panel five correctly states, the limit of the sequence is a circle. And so is this final fact: Transformation de Fourier rapide. Groupe (mathématiques) Ask a Mathematician / Ask a Physicist. Physicist: This equation ( ) was recently voted one of the most famous equations ever.
That isn’t part of the answer, it’s just interesting. Le nombre e - Historique. L’invention des logarithmes L’histoire du nombre e débute en Suisse, grâce aux travaux de John Napier (ou Neper, selon les traductions, dont le portrait est présenté ci-dessous).
Fort de ses études à la St-Andrews University, il consacre une bonne partie de sa vie à la gestion et à l’administration de ses terres. Les mathématiques le fascinent particulièrement et en 1614, il publie un manifeste qui lui prit près de vingt ans à rédiger, le Mirifici logarithorum canonis descriptio. Astroïde. ASTROÏDEAstroid, Astroide (od.

Triangle de Pascal. Premières lignes du triangle de Pascal. En mathématiques, le triangle de Pascal est une présentation des coefficients binomiaux dans un triangle. La règle à calcul. Sommaire Des objets précieuxEchelle logarithmiqueCompositionLes différentes échellesUtilisationHistorique et anecdote Si ça se trouve tu ne sais même pas ce qu’est une règle à calcul, tu n’en a peut-être jamais vu… La règle à calcul est l’ancêtre de la calculatrice, elle a été utilisée jusqu’en dans les années 60 environs, avant que la calculette électronique ne vienne la remplacer.
Elles ne sont bien sûr plus utilisées de nos jours, et ce chapitre est donc plus pour ta culture, ça ne te servira pas à grand chose pour tes études^^ Mais au moins tu verras comment on faisait auparavant sans calculatrice Les règles à calcul étaient en général vendues dans de beaux boîtiers, on pourait presque croire que ce sont des objets de collection ! Certaines règles étaient très détaillées, comme celle du bas sur l’image ci-dessous, tandis que d’autres indiquaient le stric minimum.
Comment empiler des oranges? — La conjecture de Kepler sur l’empilement des sphères. Vignette écrite par Christiane Rousseau. Orthodromie, Loxodromie. L'orthodromie est le plus court chemin pour se rendre d'un point à l'autre de la Terre On peut être surpris de voir, sur une carte, l'allure courbée des trajectoires empruntées par les vols long-courriers, ou les navires lors de grandes courses.
Cela est dû à la projection du globe terrestre, surface sphérique, sur une carte, surface plane. Cette projection induit nécessairement des déformations. La projection de Mercator est souvent utilisée, car elle respecte les angles avec les méridiens, mais en revanche elle ne respecte pas les surfaces : les régions polaires sont très fortement étirées horizontalement et verticalement (on ne peut d'ailleurs pas représenter les pôles, car ils sont rejetés à l'infini). Article Récréomath Propositions d'Alcuin. Albinus Flaccus Alcuin (735 - 804), un moine et un pédagogue, fut un des hommes les plus savants de son temps.
Pi. Un article de Wikipédia, l'encyclopédie libre. Cette page contient des caractères spéciaux. Si certains caractères de cet article s’affichent mal (carrés vides, points d’interrogation, etc.), consultez la page d’aide Unicode. Carré magique (mathématiques) Un exemple de carré magique normal d’ordre 3 et de constante magique 15. En mathématiques, un carré magique d’ordre n est composé de n2 entiers strictement positifs, écrits sous la forme d’un tableau carré. Ces nombres sont disposés de sorte que leurs sommes sur chaque rangée, sur chaque colonne et sur chaque diagonale principale soient égales. On nomme alors constante magique (et parfois densité) la valeur de ces sommes. Un carré magique normal est un cas particulier de carré magique, constitué de tous les nombres entiers de 1 à n2, où n est l’ordre du carré.
Trinh Xuan Thuan : Désir d'infini. Images des mathématiques. Le beau livre des maths De Pythagore à la 57ème dimension - cartonné - Clifford A. Pickover - Achat Livre - Achat & prix Fnac. Euclide : éléments de Géométrie (libre I) 1.