

Marine Gravity from Satellite Altimetry. Data on slight variations of the pull of gravity over the oceans are recorded with satellite altimetry, and are then combined to map the seafloor globally.

Get the Marine Gravity Map: Global Data Grids Google Earth Overlays GPlates Web Visualization Reference: Sandwell, D. Links to Related Material and Publicity Send us feedback GPlates Web Visualization These cloud-based tools are provided courtesy of Dietmar Müller on the GPlates Web Portal and require a WebGL-enabled browser. Molecular Mysticism. Shape of the Universe. The shape of the universe is the local and global geometry of the universe, in terms of both curvature and topology (though, strictly speaking, it goes beyond both).
When physicsist describe the universe as being flat or nearly flat, they're talking geometry: how space and time are warped according to general relativity. Ekpyrotic universe. Ghosting Energy: In (masking) radiation electromagnetic waves travel backwards. Sep 23, Physics/General Physics This figure shows back power flow lines at 21 GHz.

Credit: Cesar Monzon. (PhysOrg.com) -- Typically, electromagnetic waves travel away from their sources. For instance, a radar system emits radio waves that travel all the way to a target, such as a car or plane, before being reflected back to the source. Quintessence (physics) In physics, quintessence is a hypothetical form of dark energy postulated as an explanation of the observation of an accelerating rate of expansion of the Universe announced in 1998.
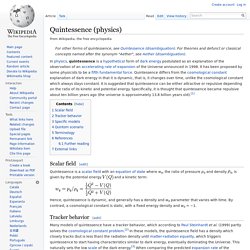
It has been proposed by some physicists to be a fifth fundamental force. Quintessence differs from the cosmological constant explanation of dark energy in that it is dynamic, that is, it changes over time, unlike the cosmological constant which always stays constant. It is suggested that quintessence can be either attractive or repulsive depending on the ratio of its kinetic and potential energy. Specifically, it is thought that quintessence became repulsive about ten billion years ago (the universe is approximately 13.8 billion years old).[1] q, is given by the potential energy and a kinetic term: Diffeomorphism. The image of a rectangular grid on a square under a diffeomorphism from the square onto itself.
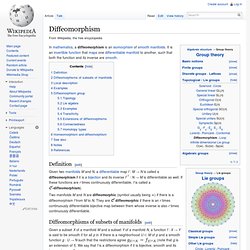
Definition[edit] Given two manifolds M and N, a differentiable map f : M → N is called a diffeomorphism if it is a bijection and its inverse f−1 : N → M is differentiable as well. If these functions are r times continuously differentiable, f is called a Cr-diffeomorphism). Two manifolds M and N are diffeomorphic (symbol usually being ≃) if there is a diffeomorphism f from M to N. They are Cr diffeomorphic if there is an r times continuously differentiable bijective map between them whose inverse is also r times continuously differentiable.
Non-orientable wormhole. In topology, this sort of connection is referred to as an Alice handle.
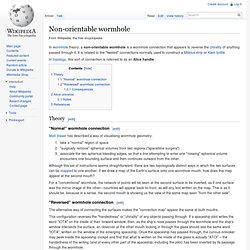
Theory[edit] "Normal" wormhole connection[edit] Matt Visser has described a way of visualising wormhole geometry: take a "normal" region of space"surgically remove" spherical volumes from two regions ("spacetime surgery")associate the two spherical bleeding edges, so that a line attempting to enter one "missing" spherical volume encounters one bounding surface and then continues outward from the other. Casimir pressure. Casimir pressure is created by the Casimir force of virtual particles.
According to experiments, the Casimir force between two closely spaced neutral parallel plate conductors is directly proportional to their surface area Therefore, dividing the magnitude of Casimir force by the area of each conductor, Casimir pressure can be found. Cabibbo–Kobayashi–Maskawa matrix. Pontecorvo–Maki–Nakagawa–Sakata matrix. In particle physics, the Pontecorvo–Maki–Nakagawa–Sakata matrix (PMNS matrix), Maki–Nakagawa–Sakata matrix (MNS matrix), lepton mixing matrix, or neutrino mixing matrix, is a unitary matrix[note 1] which contains information on the mismatch of quantum states of leptons when they propagate freely and when they take part in the weak interactions.
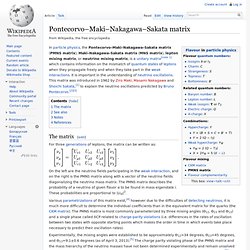
It is important in the understanding of neutrino oscillations. This matrix was introduced in 1962 by Ziro Maki, Masami Nakagawa and Shoichi Sakata,[1] to explain the neutrino oscillations predicted by Bruno Pontecorvo.[2][3] The matrix[edit] On the left are the neutrino fields participating in the weak interaction, and on the right is the PMNS matrix along with a vector of the neutrino fields diagonalizing the neutrino mass matrix. The PMNS matrix describes the probability of a neutrino of given flavor α to be found in mass eigenstate i. Based on less current data (28 June 2012) mixing angles are:[7] where NH indicates normal hierarchy and IH and. Fredkin finite nature hypothesis. In digital physics, the Fredkin Finite Nature Hypothesis states that ultimately all quantities of physics, including space and time, are discrete and finite.
All measurable physical quantities arise from some Planck scale substrate for multiverse information processing. Scharnhorst effect. The Scharnhorst effect is a hypothetical phenomenon in which light signals travel faster than c between two closely spaced conducting plates.
It was predicted by Klaus Scharnhorst of the Humboldt University of Berlin, Germany, and Gabriel Barton of the University of Sussex in Brighton, England. They showed using quantum electrodynamics that the effective refractive index, at low frequencies, in the space between the plates was less than 1 (which by itself does not imply superluminal signaling). They were not able to show that the wavefront velocity exceeds c (which would imply superluminal signaling) but argued that it is plausible.[1] Explanation[edit] Owing to Heisenberg's uncertainty principle, an empty space which appears to be a true vacuum is actually filled with virtual subatomic particles.
The effect, however, is predicted to be minuscule. Causality[edit] References[edit] Technicolor (physics) Technicolor theories are models of physics beyond the standard model that address electroweak gauge symmetry breaking, the mechanism through which W and Z bosons acquire masses. Early technicolor theories were modelled on quantum chromodynamics (QCD), the "color" theory of the strong nuclear force, which inspired their name.
In order to produce quark and lepton masses, technicolor has to be "extended" by additional gauge interactions. Particularly when modelled on QCD, extended technicolor is challenged by experimental constraints on flavor-changing neutral current and precision electroweak measurements. It is not known what is the extended technicolor dynamics. Much technicolor research focuses on exploring strongly interacting gauge theories other than QCD, in order to evade some of these challenges. Digital physics. Digital physics is grounded in one or more of the following hypotheses; listed in order of decreasing strength. The universe, or reality:
Not Even Wrong: Peter Woit's blog on General Physics. Graham Farmelo has posted a very interesting interview he did with Witten last year, as part of his promotion of his forthcoming book The Universe Speaks in Numbers. One surprising thing I learned from the interview is that Witten learned Calculus when he was 11 (this would have been 1962). He quite liked that, but then lost interest in math for many years, since no one gave him more advanced material to study. After years of studying non math/physics subjects and doing things like working on the 1972 McGovern campaign, he finally realized physics and math were where his talents lay.
He ended up doing a Ph.D. at Princeton with David Gross, starting work with him just months after the huge breakthrough of asymptotic freedom, which put in place the final main piece of the Standard Model. If only back in 1962 someone had told Witten about linear algebra and quantum mechanics, the entire history of the subject could have been quite different. Lorentz group. Pontryagin duality. In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle, or finite cyclic groups. The Pontryagin duality theorem itself states that locally compact groups identify naturally with their bidual.
Homogeneity (physics) The definition of homogeneous strongly depends on the context used. For example, a composite material is made up of different individual materials, known as "constituents" of the material, but may be defined as a homogeneous material when assigned a function. For example, asphalt paves our roads, but is a composite material consisting of asphalt binder and mineral aggregate, and then laid down in layers and compacted.
In another context, a material is not homogeneous in so far as it composed of atoms and molecules. Phase space. Phase space of a dynamic system with focal instability, showing one phase space trajectory.