

Vectores y valores propios. Calculadora de vectores propios (eigenvectores) Almost Sure – A random mathematical blog. MODNET. MODNET is an FP6 Marie Curie Research Training Network in Model Theory and its Applications, funded by the European Commission under contract number MRTN-CT-2004-512234 (MODNET).

It will run from 1 January 2005 to 31 December 2008. Vectors and the Geometry of Space. Three-Dimensional Coordinate Systems The three-dimensional coordinate system expresses a point in space with three parameters, often length, width and depth (xx, yy, and zz). Learning Objectives Identify the number of parameters necessary to express a point in the three-dimensional coordinate system Key Takeaways Key Points. When was Matrix Multiplication invented? Oliver Knill, June 7, 2009, last update, July 24, 2014 In December 2007, Shlomo Sternberg asked me when matrix multiplication had first appeared in history.

He told me about the work of Jacques Philippe Marie Binet (born February 2 1786 in Rennes and died Mai 12 1856 in Paris), who seemed to be recognized as the first to derive the rule for multiplying matrices in 1812. Shlomo also mentioned a lecture of Binet on November 30 1812 in which Binet talked about this. Here is a paper which extends Cauchy-Binet by giving a formula for the characteristic polynomial of the product of two matrices. A miniblog about this. Quantum Calculus - Calculus without limits. Oliver Knill Homepage.
Chris Staecker: Napier's Bones. Napier's Bones is an old tool used for multiplying a large number by a single digit.
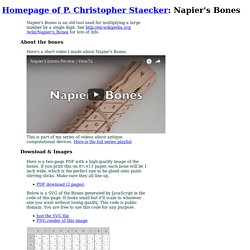
See for lots of info. About the bones Here's a short video I made about Napier's Bones. This is part of my series of videos about antique computational devices. Here is the full series playlist Download & Images Here is a two-page PDF with a high-quality image of the bones. PDF downoad (2 pages) Transforming Matrix Algebra Education for the STEM Undergraduate. Finite Geometry of the Square and Cube - Home Page. DiracDelta Science & Engineering Encyclopedia. Mathtools.net - A Resource for the Technical Computing Community.
Electronic Journal of Probability. World Web Math: Main Directory. World Web Math: Calculus Index. Mathematics Archives WWW Server. Analyse data, calculate vectors, matrices, complex numbers, quaternions, plotting. The Math Forum Internet Mathematics Library. Matrices. The Electronic Journal of Combinatorics. Einstein Institute of Mathematics @ The Hebrew University. Topics in Mathematics - Linear/Nonlinear Programming. Apuntes. Me gusta estudiar matemáticas en mis ratos libres, y mi forma de hacerlo es organizar lo que estudio en forma de libros.

Aquí está el resultado de casi todas las matemáticas que he ido estudiando en dichos ratos. Seis observaciones: Mis libros son globalmente autocontenidos: cualquier resultado utilizado en uno de ellos está demostrado en ese mismo libro o bien en otro, normalmente anterior. He recibido varios mensajes preguntándome sobre el orden más adecuado para leerlos. Aunque no están pensados para autodidactas, en teoría es posible leerlos (y entenderlos) en el orden en que aparecen, si bien en la práctica también es posible (y en muchos casos recomendable) empezar por los libros de álgebra, geometría y análisis I y seguir en orden a partir de ahí, ya que los libros anteriores son mucho más técnicos y no son necesarios para seguir los que vienen después.
Apuntes. Pauls Online Math Notes. The Ultimate Online Reference for Engineers. Euclid's Elements, Introduction. Euclid’s Elements form one of the most beautiful and influential works of science in the history of humankind.
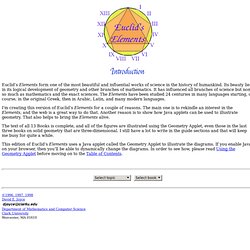
Its beauty lies in its logical development of geometry and other branches of mathematics. It has influenced all branches of science but none so much as mathematics and the exact sciences. The Elements have been studied 24 centuries in many languages starting, of course, in the original Greek, then in Arabic, Latin, and many modern languages. I'm creating this version of Euclid’s Elements for a couple of reasons. The main one is to rekindle an interest in the Elements, and the web is a great way to do that. The text of all 13 Books is complete, and all of the figures are illustrated using the Geometry Applet, even those in the last three books on solid geometry that are three-dimensional. This edition of Euclid’s Elements uses a Java applet called the Geometry Applet to illustrate the diagrams.
MacTutor History of Mathematics. Touch Mathematics. Geogebra. Gacetilla matematica. Dave's Short Trig Course. Table of Contents Who should take this course?

Trigonometry for you Your background How to learn trigonometry Applications of trigonometry Astronomy and geography Engineering and physics Mathematics and its applications What is trigonometry? Trigonometry as computational geometry Angle measurement and tables Background on geometry The Pythagorean theorem An explanation of the Pythagorean theorem Similar triangles Angle measurement The concept of angle Radians and arc length Exercises, hints, and answers About digits of accuracy Chords What is a chord? Ptolemy’s sum and difference formulas Ptolemy’s theorem The sum formula for sines The other sum and difference formulas Summary of trigonometric formulas Formulas for arcs and sectors of circles Formulas for right triangles Formulas for oblique triangles Formulas for areas of triangles Summary of trigonometric identities More important identities Less important identities Truly obscure identities About the Java applet.
Math Problem Solver. DLMF: Geometry & Topology. {7,3,3} Honeycomb Meets Plane at Infinity. {7,3,3} Honeycomb Meets Plane at Infinity – Roice Nelson This picture by Roice Nelson shows the boundary of the {7,3,3} honeycomb, the shape featured in our last article: • {7,3,3} honeycomb.

The black circles are holes, not contained in the boundary of the {7,3,3} honeycomb. There are infinitely many holes, and the actual boundary, shown in white, is a fractal with area zero. The {7,3,3} honeycomb lives in 3-dimensional hyperbolic space, a space that can be fit inside a ball using the Poincaré ball model. Roice Nelson used stereographic projection to draw part of the surface of the Poincaré ball as a plane: the plane at infinity. Conformal Geometry and Dynamics. Journals. AMS peer-reviewed journals are of the highest quality in mathematical research.
Our journals have been published since 1891 and cover a broad range of mathematics. Each journal is managed by editors who are prominent in their fields, and each is unique in its offering of articles, book reviews, and reports. In addition to publishing and distributing printed journals, the AMS offers searchable electronic versions that are available prior to the print versions. When the journal is available in electronic format, the electronic version is considered the version of record. Browse our current subscription rates. Divulgaciones Matematicas. Boletín de la Asociación Matemática Venezolana. This is the electronic version of the Bulletin of the Venezuelan Mathematical Association (AMV).

There exist a printed version which is published twice a year. ELibM: Mathematical Journals. Archived, dormant, or outdated journal pages This section lists journals whose content is not updated anymore within EMIS, in particular those whose current offers have been moved to other publishing locations.

Advances in Difference EquationsThe journal continues to be available from Springer. The EMIS holdings comprise Vols. 2004–2011.Advances in GeometryThe journal continues to be available from de Gruyter's ReferenceGlobal website. The EMIS holdings comprise Vols. 1–4 (2001–2004).AMA Algebra Montpellier Announcements/Annonces de Montpellier en AlgèbreThe journal has ceased publication. The EMIS holdings comprise all issues which have published.Algebraic & Geometric TopologyThe journal continues to be available from Geometry and Topology Publications.
Annals of Functional Analysis (AFA) Interactive Mathematics Miscellany and Puzzles. Alpha: Computational Knowledge Engine.