

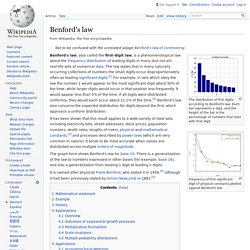
Benford's law. The distribution of first digits, according to Benford's law.
Entropy (information theory) 2 bits of entropy.
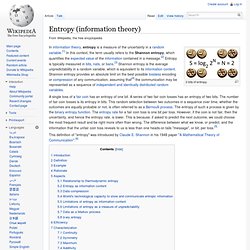
A single toss of a fair coin has an entropy of one bit. A series of two fair coin tosses has an entropy of two bits. The number of fair coin tosses is its entropy in bits. This random selection between two outcomes in a sequence over time, whether the outcomes are equally probable or not, is often referred to as a Bernoulli process. 0511171. Interesting number paradox. The interesting number paradox is a semi-humorous paradox which arises from the attempt to classify natural numbers as "interesting" or "dull".
The paradox states that all natural numbers are interesting. The "proof" is by contradiction: if there exists a non-empty set of uninteresting numbers, there would be a smallest uninteresting number – but the smallest uninteresting number is itself interesting because it is the smallest uninteresting number, producing a contradiction. Paradoxical nature[edit] Attempting to classify all numbers this way leads to a paradox or an antinomy of definition. Any hypothetical partition of natural numbers into interesting and dull sets seems to fail. Pontryagin's minimum principle. Pontryagin's maximum (or minimum) principle is used in optimal control theory to find the best possible control for taking a dynamical system from one state to another, especially in the presence of constraints for the state or input controls.
Calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points.
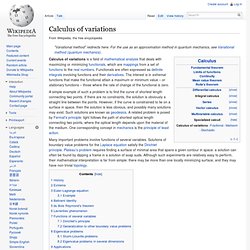
If there are no constraints, the solution is obviously a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as geodesics.
Sophomore's dream. Discovered in 1697 by Johann Bernoulli.
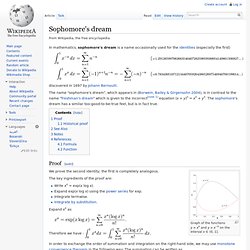
The name "sophomore's dream", which appears in (Borwein, Bailey & Girgensohn 2004), is in contrast to the name "freshman's dream" which is given to the incorrect[note 1] equation (x + y)n = xn + yn. The sophomore's dream has a similar too-good-to-be-true feel, but is in fact true. Proof[edit] Freshman's dream. An illustration of the Freshman's dream in two dimensions.
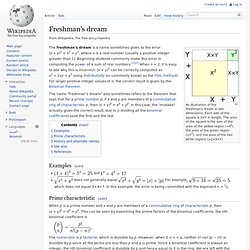
Each side of the square is X+Y in length. The area of the square is the sum of the area of the yellow region (=X2), the area of the green region (=Y2), and the area of the two white regions (=2×X×Y). The freshman's dream is a name sometimes given to the error (x + y)n = xn + yn, where n is a real number (usually a positive integer greater than 1). Beginning students commonly make this error in computing the power of a sum of real numbers.[1][2] When n = 2, it is easy to see why this is incorrect: (x + y)2 can be correctly computed as x2 + 2xy + y2 using distributivity (or commonly known as the FOIL method). Cantor's diagonal argument. An illustration of Cantor's diagonal argument (in base 2) for the existence of uncountable sets.
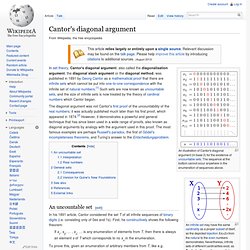
The sequence at the bottom cannot occur anywhere in the enumeration of sequences above. An infinite set may have the same cardinality as a proper subset of itself, as the depicted bijectionf(x)=2x from the natural to the even numbers demonstrates. Nevertheless, infinite sets of different cardinalities exist, as Cantor's diagonal argument shows. In set theory, Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural numbers.[1] Such sets are now known as uncountable sets, and the size of infinite sets is now treated by the theory of cardinal numbers which Cantor began.
An uncountable set[edit] Russell's paradox. In the foundations of mathematics, Russell's paradox (also known as Russell's antinomy), discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction.
The same paradox had been discovered a year before by Ernst Zermelo but he did not publish the idea, which remained known only to Hilbert, Husserl and other members of the University of Göttingen. In 1908, two ways of avoiding the paradox were proposed, Russell's type theory and the Zermelo set theory, the first constructed axiomatic set theory. Zermelo's axioms went well beyond Frege's axioms of extensionality and unlimited set abstraction, and evolved into the now-canonical Zermelo–Fraenkel set theory (ZF).[1] Informal presentation[edit] Now we consider the set of all normal sets, R. Formal presentation[edit] and the following axiom schema of unrestricted comprehension: for any formula P with only the variable x free.
For . Berry paradox. The Berry paradox is a self-referential paradox arising from an expression like "the smallest positive integer not definable in fewer than twelve words" (note that this defining phrase has fewer than twelve words).
Bertrand Russell, the first to discuss the paradox in print, attributed it to G. G. Berry (1867–1928),[1] a junior librarian at Oxford's Bodleian library, who had suggested the more limited paradox arising from the expression "the first undefinable ordinal". Gödel's incompleteness theorems. Gödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of mathematics. The two results are widely, but not universally, interpreted as showing that Hilbert's program to find a complete and consistent set of axioms for all mathematics is impossible, giving a negative answer to Hilbert's second problem.
The first incompleteness theorem states that no consistent system of axioms whose theorems can be listed by an "effective procedure" (i.e., any sort of algorithm) is capable of proving all truths about the relations of the natural numbers (arithmetic). For any such system, there will always be statements about the natural numbers that are true, but that are unprovable within the system. Background[edit] First incompleteness theorem[edit] Diagonalization[edit] B. Random walk. Example of eight random walks in one dimension starting at 0. The plot shows the current position on the line (vertical axis) versus the time steps (horizontal axis). A random walk is a mathematical formalization of a path that consists of a succession of random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the financial status of a gambler can all be modeled as random walks, although they may not be truly random in reality.
The term random walk was first introduced by Karl Pearson in 1905.[1] Random walks have been used in many fields: ecology, economics, psychology, computer science, physics, chemistry, and biology.[2][3][4][5][6][7][8][9] Random walks explain the observed behaviors of processes in these fields, and thus serve as a fundamental model for the recorded stochastic activity. Various different types of random walks are of interest. . . Lattice random walk[edit] . Slumpvandring_eng. Abc conjecture. Lagrange multiplier. Figure 1: Find x and y to maximize f(x, y) subject to a constraint (shown in red) g(x, y) = c.
Figure 2: Contour map of Figure 1. Normal. Generalized continued fraction. In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values. Euler's continued fraction formula. In the analytic theory of continued fractions, Euler's continued fraction formula is an identity connecting a certain very general infinite series with an infinite continued fraction. First published in 1748, it was at first regarded as a simple identity connecting a finite sum with a finite continued fraction in such a way that the extension to the infinite case was immediately apparent.[1] Today it is more fully appreciated as a useful tool in analytic attacks on the general convergence problem for infinite continued fractions with complex elements.
Density_of_primes.