

Graph Theory. Informally, a graph is a diagram consisting of points, called vertices, joined together by lines, called edges; each edge joins exactly two vertices.

A graph G is a triple consisting of a vertex set of V(G), an edge set E(G), and a relation that associates with each edge two vertices (not necessarily distinct) called its endpoints. Definition of Graph. InterestingSurfaces.nb. Interesting Surfaces.

How to Rotate a Vertex by a Quaternion in GLSL (*Updated*) – Geeks3D. In a vertex shader, the rotation and position are usually encoded in the model matrix and we have something like this:

An MGS Graphic Gallery. Exploring Multivariable Calculus. And then relaunch Chrome.
Instructors: If you are an instructor using this project in any way, please send me an email to let me know of your interest. I would love to see more people using the materials from this project, and it is important that I be able to report how the project is doing to the NSF. I also encourage anyone who is interested in this project to take the time to write something on the discussion board. You will need to become a member to do this, but I am the only one who will see this member information. It is a private website, and membership makes it easier to keep spam from being placed on the discussion board. The following PDF documents give more information about the goals and current state of the project. 9-27-2011 Graph implicit equations in spherical or cylindrical coordinates like rho^2 = -sec(2ϕ) or r^2*theta^2 = r +theta.Implicit surfaces/equations can now be graphed in spherical and cylindrical coordinates as well as in cartesian coordinates.
June 29, 2011. Hugi 27 - coding corner polaris sphere tessellation 101. Sphere Tessellation 101: "The Art of Making Spheres out of Triangles" By Polaris / Northern Dragons Dedication: To My Father, Celebrating his 66th Birthday – June 3rd.

Introduction. Objet 3D - supertos.free.fr. Introduction Comme ce chapitre porte bien sont nom...
Nous allons avoir besoin de 2 différents objets près pour un affichage 3D sous OpenGL: - La sphère - Le cube. Pour y parvenir, nous allons utiliser la conception d'objet en partant de ceci: Pour la sphère : la sphère est une pécialisation d'un sphéroïde qui est lui même une spécialisation des quadriques qui sera une spécialisation de Objet3d. Unity - Algorithm for creating spheres? Creating 3D graphics. The aim of this tutorial is to explain how to create basic 3D graphics.
It uses the Khan Academy Computer Science platform, but the principles are the same no matter what graphics program you use. I used the HTML5 Canvas and very similar code to make the 3D examples on this page. These platforms is not really designed for 3D graphics, but that just means we can write our own 3D graphics engine and, in doing so, learn a bit how 3D graphics work (and why there is a reason to learn trigonometry). What are 3D graphics? Three parallelograms pretending to be a cube. Since computer screens are essentially two-dimensional, 3D graphics are just 2D optical illusions that trick your brain into thinking it is seeing a 3D object. A 3D graphics engine works by calculating what 2D shapes a 3D object would project on to the screen. Representing shapes. Source1. Mesh Processing — Images (Image processing, digital and computational geometry) 2014.0.
Mesh representation Overview Rough definition.
Tutorial #3: The icosahedron-based geodesic sphere. The content that follows was originally published on the Don Havey website at This quick tutorial will show a more reasonable alternative to the electronsphere, which addressed the problem of distributing points evenly on a sphere.

We’ll be creating a geodesic sphere (like at the Epcot center) using a subdivided icosahedron. It’s a relatively simple script and inexpensive in terms of CPU usage. Much more efficient than the electronsphere approach, though not quite as interesting. And here are the classes you’ll need: Icosahedron classes. GEO Editor. GEO Editor is an online platonic solids editor written in WebGL and based on custom half edge mesh implementation.
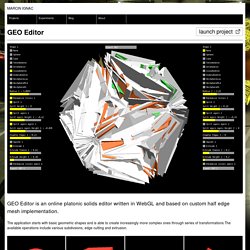
The application starts with basic geometric shapes and is able to create increasingly more complex ones through series of transformations The available operations include various subdivsions, edge cutting and extrusion. Basic shapes More complex structures Chamfer edges Random colors Inside of the mesh The GEO editor running in a web browser Collaboration with GMUNK. What are map projections? Part54. Riemann for Anti-Dummies Part 54 To understand Riemann's treatment of Abelian functions, situate that discovery within the context of the history in which it arose, reaching back to the pre-Euclidean Pythagoreans of ancient Greece, and forward to LaRouche's unique and revolutionary discoveries in the science of physical economy. Imagine that entire sequence, all at once, as a dramatic history, leap over time, project the past into the future, the future into the past, and both into the present, so that centuries of accomplishment are telescoped into a single, instantaneous thought.
Dynamis In the opening scene of Plato's {Theatetus} dialogue, Euclides of Megara informs Terpsion that he has just seen Theatetus being carried to Athens, near death, after being wounded in the battle at Corinth.