

Five Triangles: 248. Semicircle bow tie. Five Triangles: 246. Semicircle section. Euclidean Algebra. FMSP Algebra Problems. Dy/dan » Blog Archive » If Exponent Rules Are Aspirin, Then What Is The Headache? This Week’s Skill Exponent Rules.
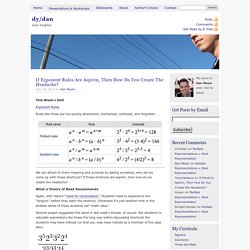
Rules like these are too quickly abstracted, memorized, confused, and forgotten. We can attach to them meaning and purpose by asking ourselves, why did we come up with these shortcuts? If these shortcuts are aspirin, then how do we create the headache? What a Theory of Need Recommends Again, with Harel’s “need for computation,” students need to experience the “longcut” before they learn the shortcut. Several people suggested the same in last week’s thread, of course. Chris Hulitt was one of my workshop participants in Norristown, PA, and his group suggested an important addition to this idea. Looks the same as the last, right? Again, this isn’t real world, or relevant, per our usual definitions of the term. Next Week’s Skill.
Book of Proof. FMSP Co-ordinate Geometry Problems. Choose Three Numbers. FMSP Problem Solving 1. FMSP Algebra Problems. FMSP Quadratics and Cubics Problems. Proof of rectangle areas on square grid using surds. MathArguments180.com: 481: Two Circles and One Square. Exponetial Function Card Sort. Dy/dan » Blog Archive » If Graphing Linear Inequalities Are Aspirin, Then How Do You Create The Headache?
This Week’s Skill Here is the first paragraph of McGraw-Hill’s Algebra 1 explanation of graphing linear inequalities: The graph of a linear inequality is the set of points that represent all of the possible solutions of that inequality.
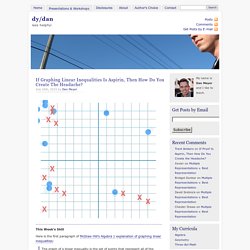
An equation defines a boundary, which divides the coordinate plane into two half-planes. This is mathematically correct, sure, but how many novices have you taught who would sit down and attempt to parse that expert language? The text goes on to offer three steps for graphing linear inequalities: Graph the boundary. The text offers aspirin for a headache no one has felt. The shading of the half-plane emerges from nowhere. We can fix that. MathArguments180.com: 484: Tempus Fugit. Difference of two squares- visual representation. Dy/dan » Blog Archive » If Functions Are Aspirin, Then How Do You Create The Headache? This Week’s Skill Determining if a relationship is a function or not.
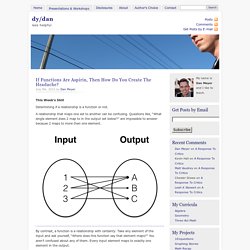
A relationship that maps one set to another can be confusing. Questions like, “What single element does 2 map to in the output set below?” Are impossible to answer because 2 maps to more than one element. By contrast, a function is a relationship with certainty. Pearson and McGraw-Hill’s Algebra 1 textbooks simply provide a definition of a function. Parallel Lines. Exponent+picture.png (PNG Image, 481 × 257 pixels) Dy/dan » Blog Archive » If Proof Is Aspirin, Then How Do You Create the Headache? This Week’s Skill Proof.
This is too big for a blog post, obviously. What a Theory of Need Recommends If proof is the aspirin, then doubt is the headache. In school mathematics, proof can feel like a game full of contrived rules and fragile pieces. Prove angle B is congruent to angle D.Prove triangle BCD is congruent to triangle ACB.Decide if angle B and angle C are congruent. One of those proof prompts is not like the others. The act of proving has many purposes. Integration Lesson Ideas (TLP) Reason and Wonder. As is often the case when a school year winds down, a few ideas have crept into my head that I wish I’d have thought of eight months earlier.
Things are winding down quickly at my school (seniors are done with classes; junior high wraps up this Friday; and high school next Friday), so I’ll share this here in case it’s of use to anyone whose year stretches into June—or for anyone interested in giving this a run in the fall. Step 1. Throw this in front of your students: Step 2.
Give students some think time. If you have enough whiteboard space, give the entire class 60 seconds to write one of their equations on the board. Trigonometric Ratios - Interactive Graph. Resourceaholic: New GCSE: Sequences. I've been busy getting my head around the additional sequences content in the new 9 - 1 Maths GCSE and thought it would be helpful to share my findings.

Quite a lot has been added to the higher tier. Previously students covered all the GCSE sequences content at Key Stage 3 so there was nothing new to teach at Key Stage 4. But now we need to include a few weeks' worth of sequences lessons in our GCSE schemes of work. Functions puzzle.png (598×334) Inequalities.png (600×248) Differentiation.png (598×265) Mathematics, Learning and Technology. A previous post on Functions features resources aimed at older students; I thought it would be useful to look at resources for teaching younger students.
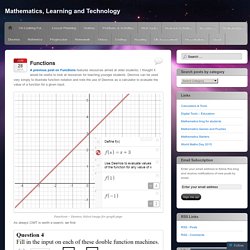
Desmos can be used very simply to illustrate function notation and note the use of Desmos as a calculator to evaluate the value of a function for a given input. Functions – Desmos. Select image for graph page. Mr Collins Mathematics Blog: Simplifying Surds Task/Resource. A couple of weeks ago I was teaching Surds to my Y9 class (doing the new Edexcel 1-9 GCSE Spec).
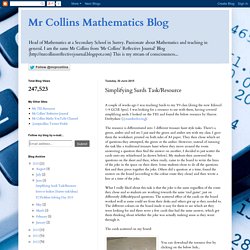
I was looking for a resource to use with them, having covered simplifying surds. I looked on the TES and found the below resource by Sharon Derbyshire (@numberloving). The resource is differentiated into 3 different treasure hunt style tasks. There's a green, amber and red set. Mr Collins Mathematics Blog: Intro to Indices (Starter task/idea) After the May half term we set our Y9s according to Edexcel's 'Baseline Tests' for their new 1-9 GCSE Spec.
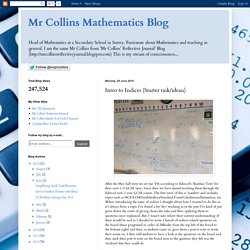
Since then we have started teaching them through the Edexcel new 2 year GCSE course. The first 'unit' of this is 'number' and includes topics such as HCF/LCM/Surds/Indices/Standard Form/Calculations/Estimation, etc. When introducing the topic of indices I thought about how I wanted to do this as it's always been a topic I've found a bit 'dry' teaching as in the past I've kind of just gone down the route of giving classes the rules and then applying them to questions once explained.
But, I wasn't sure where their current understanding of these would be and so I decided to write a bunch of indices related questions on the board (these progressed in order of difficulty from the top left of the board to the bottom right) and then, as students came in, gave them a post-it note to write their name on. Dy/dan » Blog Archive » If Factoring Trinomials is Aspirin Then How Do You Create The Headache? This Week’s Skill Factoring quadratic trinomials. eg.
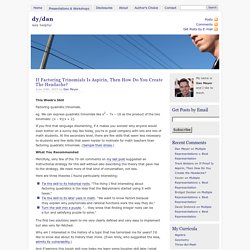
We can express quadratic trinomials like x2 – 7x – 18 as the product of the two binomials: (x – 9)(x + 2). If you find that language disorienting, if it makes you wonder why anyone would even bother on a sunny day like today, you’re in good company with lots and lots of math students. At the secondary level, there are few skills that seem less necessary to students and few skills that seem harder to motivate for math teachers than factoring quadratic trinomials.
Area Problem #20. Coordinate Problem #2. Forming and Solving Quadratics (TLP) Long Division. Factorising Quadratic Equations: In Steps. Pizza Doubler. Prologue act one 1. Continuous Everywhere but Differentiable Nowhere. Matt Enlow (math teacher in MA) posted a fascinating problem online today, one he thinks of when storing all those plastic bags from the grocery store. You shove them so they all lie in a single bag, and throw that bag under the sink. Here’s the question: how many different ways can you store these bags? For 1 bag, there is only 1 way. For 2 bags, there is still only 1 way. Negative and fractional indices treasure hunt - Algebra - Indices – index laws - Dominoes, loop cards and treasure hunts - Search results - Search. Published: 30/08/2013KS4 KS5 3 pages Negative and fractional indices treasure hunt This resource combines a treasure hunt with a code breaking activity to test students' index and substitution skills!
Simplify each expression to create a loop of 15 cards, then substitute in values for x and y to decipher the hidden message. Expressions range from simple multiplications to algebraic fractions and raising brackets to a power. Download the adaptable Word resource. Fractional & negative indices. Roots and Indices Maze. Indices - National STEM Centre. MathArguments180.com: 449: Fractions. Straight line arithmagons.png (640×342) Gradient.png (598×254) Simplifying Radicals: Tug of War - Evaluating Expressions Game. @mathhombre pointed me in the direction of this interesting Tug of War game. Click here. I was playing around with the idea to make it more mathy, and here is what I came up with.
I thought trading cards would be fun and each card looks something like this: Each card would have a function in the top left corner. The game could start with linear functions, and then mix in cards with other functions. In the top right is the suit. In the middle is the character. The arrows indicated in which direction the character can get his strength. Each player places up to 9 characters in a 3x3 array. Let's suppose that this card is placed on the bottom left of your 3x3 array. Following on from my last post on ideas for the first Year 7 lesson of the year, here's some ideas for the start of Year 12. Power is an illusion. Powers, roots and index laws - Resources - TES. Power List.
» The burden of proof. On the back of an earlier post on Transforming Functions, I thought I might share some other A/A* lessons I have taught recently. Please note, what has worked well for me and my students, may not work well for you and your students. The idea of the post is to give people a starting point and if it inspires just one idea, then it has been worthwhile! I would also be interested in other people’s ideas/approaches, please use the comments section below to share these. Also, if you are just looking for resources on proof, try Jo Morgan’s ()fantastic resourceaholic website. MEDIAN Don Steward secondary maths teaching: rearrangement steps. Simplifying Radicals: Absolute Value INEQUALITY Game. THE proof! See²! 271. Bored with exponentials. Maths ROTW 83 - Quadratics - Mathematics teaching - TES Mathematics - TES Community.
Core AS. This page lists recommended resources for teaching Core Mathematics at AS level, categorised by topic. Huge thanks to all individuals and organisations who share teaching resources.Indices. Resourceaholic: Core A2. Pages. 10 Calculator Buttons you need in your life #revision #gcse #alevel. Trigonometry Graph Matching - Google Docs. Areas of Sectors (TLP) Trigonometry and the Double-Angle Formulae. MEDIAN Don Steward secondary maths teaching: self-inverse and periodic functions. Functions. Axis. Simplifying Radicals: Writing Linear Equations Given Two Ordered Pairs.
Perpendicular Lines. Resourceaholic: Tricks and Tips 2: Sequences, Linear Graphs and Surds. Equations of Lines (TLP) 270. A whiff of cheese and exponentials. Logarithms. MEDIAN Don Steward secondary maths teaching: geometric series, some with surds. Resourceaholic: Tricks and Tips 2: Sequences, Linear Graphs and Surds. FMSP, Sequence and Series Problems. Geometric Sequence Sort Cards. Geometric Sequences Worksheet. Visual Patterns.
First Steps to Differentiation. Resourceaholic: Introducing Differentiation. Deriving%20the%20product%20rule.pdf. A level Maths C1: Differentiation Worksheets - Resources - TES. Solve My Maths. The Surdinator. Resourceaholic: Tricks and Tips 2: Sequences, Linear Graphs and Surds. Surds Pythag 2.jpg (598×319) Solve My Maths. Surds. Solve My Maths. Root it Out. Trigonometric Identities.
FMSP Function Problems. Quadratics Functions and Expressions. Pythagorean Triples. Categorising Quadratic Curves. Factorising Quadratics (TLP) Resourceaholic: Tricks and Tips 3: Quadratics. Vectors. 3D printing and the quadratic curve. N11 Manipulating surds.