

Popularity contest - Tweetable Mathematical Art - Programming Puzzles & Code Golf Stack Exchange. OK, this one gave me a hard time.
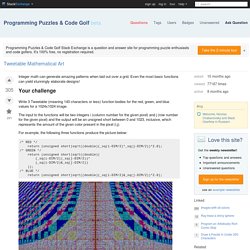
I think it's pretty nice though, even if the results are not so arty as some others. That's the deal with randomness. Maybe some intermediate images look better, but I really wanted to have a fully working algorithm with voronoi diagrams. This is one example of the final algorithm. The image is basically the superposition of three voronoi diagram, one for each color component (red, green, blue). Code ungolfed, commented version at the end unsigned short red_fn(int i, int j){int t[64],k=0,l,e,d=2e7;srand(time(0));while(k<64){t[k]=rand()%DIM;if((e=_sq(i-t[k])+_sq(j-t[42&k++]))<d)d=e,l=k;}return t[l];} unsigned short green_fn(int i, int j){static int t[64];int k=0,l,e,d=2e7;while(k<64){if(!
It took me a lot of efforts, so I feel like sharing the results at different stages, and there are nice (incorrect) ones to show. First step: have some points placed randomly, with x=y Second: have a better y coordinate 3rd: I don't remember but it's getting nice 4th: scanlines. Yann LeCun's Research and Contributions. Things I worked on.

Current Projects PhD During my PhD, in 1985, I proposed and published (in French), an early version of the learning algorithm known as error backpropagation[LeCun, 1985][LeCun, 1986]. Although a special form of my algorithm was equivalent to backpropagation it was based on backpropagating "virtual target values" for the hidden units rather than gradients. I had actually proposed the algorithm during my Diplome d'Etudes Approfondies work in 1983/1984 but had no theoretical justification for it back then. At the end of my PhD, my friend Leon Bottou and I started writing a software system called SN to experiment with machine learning and neural networks.
Cnd.mcgill.ca/~ivan/miniref/linear_algebra_in_4_pages.pdf. Linear Algebra tutorial. By Kardi Teknomo, PhD.
Share this: Google+ In this simple Linear Algebra tutorial, you will review the basic operations on vectors, matrices, solving linear equations and eigen systems. I made free educational interactive programs online for almost every topic. The programs are well suited to guide discovery experiences where you can focus on the concept of linear algebra and let the program compute the more complex calculation. My focus is to introduce linear algebra with clarity of explanation. First, take a look on how to input a vector or a matrix in the interactive program, and then you can select the topics below that you are not familiar or you want to review. If you are a first time learners, who are not familiar with most of the topics, you should browse each section & each topic of the tutorial in sequence.
The strength of linear algebra lies on the properties of each operation. Here are the topics of this linear algebra tutorial: What is Vector? Matrix Algebra Is Equal Matrix? Interactive Activation & Competition (Built with Processing) This applet is a demonstration of "Interactive Activation and Competition" neural networks, as first described by J.L.
McClelland in the following paper: McClelland, J.L. (1981). Retrieving general and specific information from stored knowledge of specifics. Proceedings of the Third Annual Meeting of the Cognitive Science Society, 170-172. A more complete description of the network is also available in Rumelhart, D.E., McClelland, J.L., and the PDP research group (1986).Parallel Distributed Processing Volume 1: Foundations, MIT Press.
The model was a landmark illustration of how simple networks of interconnected elements (artificial neurons, so to speak) can be organized so as to form a memory system that exhibits several crucial properties of human memory, including The simple system nevertheless exhibits complex dynamics of interaction and competition as activation spreads through the network in response to your input. --axel cleeremans (home page) Take a personality test. Morituri Salutamus: Poem for the Fiftieth Anniversary of the Class of 1825 in Bowdoin College by Henry Wadsworth Longfellow.
Tempora labuntur, tacitisque senescimus annis, Et fugiunt freno non remorante dies.
Ovid, Fastorum, Lib. vi. "O Cæsar, we who are about to die Salute you! " was the gladiators' cry In the arena, standing face to face With death and with the Roman populace. O ye familiar scenes,—ye groves of pine, That once were mine and are no longer mine,— Thou river, widening through the meadows green To the vast sea, so near and yet unseen,— Ye halls, in whose seclusion and repose Phantoms of fame, like exhalations, rose And vanished,—we who are about to die, Salute you; earth and air and sea and sky, And the Imperial Sun that scatters down His sovereign splendors upon grove and town. Ye do not answer us! We are forgotten; and in your austere. Yann LeCun's Research and Contributions. Beau Lotto: Optical illusions show how we see.