Mathematicians Make a Major Discovery About Prime Numbers. Paul Erdős, left, and Terence Tao discussing math in 1985. This past August, Tao and four other mathematicians proved an old Erdős conjecture, marking the first major advance in 76 years in understanding how far apart prime numbers can be. Olena Shmahalo / Quanta Magazine; original courtesy of Terence Tao In May 2013, the mathematician Yitang Zhang launched what has proven to be a banner year and a half for the study of prime numbers, those numbers that aren’t divisible by any smaller number except 1. Zhang, of the University of New Hampshire, showed for the first time that even though primes get increasingly rare as you go further out along the number line, you will never stop finding pairs of primes that are a bounded distance apart — within 70 million, he proved.
Now, mathematicians have made the first substantial progress in 76 years on the reverse question: How far apart can consecutive primes be? Olena Shmahalo / Quanta Magazine Eleanor Grant. The world's largest prime number — visualized. Images: The World's Most Beautiful Equations | Beauty of Math. Jacquard looms: Videos demonstrating early computer programs. Invented in 1801, Jacquard looms are really an add-on to already existent mechanical loom systems, which allowed those looms to create patterns more complex and intricate than anything that had been done before.
The difference: Punch cards. When you weave, the pattern comes from changes in thread position — which threads were exposed on the surface of the cloth and which were not. But prior to the Jacquard loom, there were only so many threads that any weaver could control at one time, so patterns were simple and blocky.
Essentially, the Jacquard system vastly increased the pixels available in any weaving pattern, by automatically controlling lots and lots of threads all at once. Punch cards told the machine which threads were in play at any given time. It's a really cool process, and I wanted to share a couple of videos that give you a good idea of how these looms work and how they changed the textiles industry. You can watch them below. Rolling Hypocycloids. The hypocycloid with n cusps is the curve traced out by a point on a circle rolling inside a circle whose radius is n times larger.
The hypocycloid with 2 cusps is sort of strange: It’s just a line segment! It’s called the Tusi couple. The hypocycloid with 3 cusps is called the deltoid, because it’s shaped like the Greek letter Δ: The hypocycloid with 4 cusps is called the astroid, because it reminds people of a star: I got interested in hypocycloids while writing some articles here: • Rolling circles and balls. My goal was to explain a paper John Huerta and I wrote about the truly amazing things that happen when you roll a ball on a ball 3 times as big.
While pondering hypocycloids in the ensuing discussion, the mathematician, physicist, programmer and science fiction author Greg Egan created this intriguing movie: It’s a deltoid rolling inside an astroid. Why does it work? SU(n) is the group of n × n unitary matrices with determinant 1. For the details, see this article on my other blog: Infinity Imagined. Infinity Imagined. Infinity Imagined. Infinity Imagined. This well-known Egyptian symbol is actually an early math problem. Hartverdrahtet – Infinite complexity in 4096 Bytes - winner of the PC 4kB intro comp. Worthy winner of the PC 4kB intro competition at Revision 2012 and latest example of the compact-coding tradition exercised within the demoscene, Hartverdrahtet by Akronyme Analogiker is a three minute long audio-visual trip into a procedural fractalverse, compressed into a minuscule piece of software.
No bigger than 4096 bytes – less than an empty Word document, as demoscene activists like to point out – the executable file contains all the mathematics needed to generate the unfolding visual complexity and audible ambience upon a double-click. A solo effort by a talented coder who calls himself Demoscene Passivist, Hartverdrahtet reveals a mesmerizing cosmos observed through what could be an electron microscope – ethereal, greenish and a little eerie. The real magic is in the lingo: “It’s a mix of shere-tracing, fake ambient occlusion and a lot of post-processing. Hartverdrahtet runs on Windows XP/Vista/7 (fast CPU/GPU adviced) and can be downloaded here.
5 Seriously Mind-Boggling Math Facts. By Natalie Wolchover | January 25, 2013 07:19am ET Credit: public domain Mathematics is one of the only areas of knowledge that can objectively be described as "true," because its theorems are derived from pure logic. And yet, at the same time, those theorems are often extremely strange and counter-intuitive. Some people find math boring. As these examples show, it's anything but.
Cool Math Games | Math Cats, B-Cubed, First in Math, IXL Math. Doodling in Math Class: Connecting Dots. The Mathematical Art Of M.C. Escher. The Fibonacci in Lateralus. The Fibonacci Sequence. How do japanese multiply?? How To: 1 x 8 1=9 - Beauty of Mathematics | SialNity.Com. The Coastline Paradox & The Koch Snowflake. The nature of nothingness. Zilch… Naught… Nada… It’s easy to dismiss the concept of nothing as, well, nothing. In fact, nothing is everything to science – understanding the intangible voids has lead to breakthroughs we could never have imagined possible. Read on to find out why nothing is more important than nothing… Nothingness: Zero, the number they tried to ban Every schoolchild knows the concept of zero – so why did it take so long to catch on?
Follow its convoluted path from heresy to common sense Read more: "The nature of nothingness" I USED to have seven goats. This is not a trick question. This is a tangled story of two zeroes: zero as a symbol to represent nothing, and zero as a number that can be used in calculations and has its own mathematical properties. Zero the symbol was in fact the first of the two to pop up by a long chalk. It is through such machinations that the string of digits "2012" comes to have the properties of a number with the value equal to 2 × 103 + 0 × 102 + 1 × 101 + 2. What are Amicable Numbers? Los socorridos números de Fibonacci.
La secuencia de Fibonacci es una sucesión infinita de números naturales. Se denominan así los números que permiten contar los elementos de un conjunto. Son el primer grupo de números que fueron usados por los seres humanos para contar cosas. El uno, el dos, el cinco, por nombrar algunos, son números naturales. En la secuencia de Fibonacci cada número viene dado por la suma de los dos anteriores.
Cierto hombre tenía una pareja de conejos juntos en un lugar cerrado y desea saber cuántos son creados a partir de este par en un año cuando es su naturaleza parir otro par en un simple mes, y en el segundo mes los nacidos parir también Esta secuencia numérica se ha hecho muy conocida en la cultura popular, podemos encontrar referencias a la misma en libros, canciones, películas y series de televisión. Series de televisión En Fringe la secuencia ha aparecido varias veces.
En el drama procedimental Criminal Minds un asesino usa la secuencia de Fibonacci para encontrar a sus víctimas. Películas. Bifurcation diagram. In mathematics, particularly in dynamical systems, a bifurcation diagram shows the possible long-term values (equilibria/fixed points or periodic orbits) of a system as a function of a bifurcation parameter in the system.
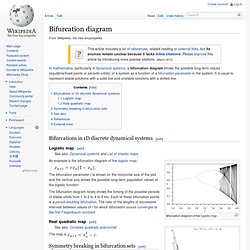
It is usual to represent stable solutions with a solid line and unstable solutions with a dotted line. Bifurcations in 1D discrete dynamical systems[edit] Logistic map[edit] Animation showing the formation of bifurcation diagram An example is the bifurcation diagram of the logistic map: The bifurcation parameter r is shown on the horizontal axis of the plot and the vertical axis shows the possible long-term population values of the logistic function. The bifurcation diagram nicely shows the forking of the possible periods of stable orbits from 1 to 2 to 4 to 8 etc. Real quadratic map[edit] The map is Symmetry breaking in bifurcation sets[edit] In a dynamical system such as which is structurally stable when , if a bifurcation diagram is plotted, treating , the case See also[edit] Four color theorem. Example of a four-colored map A four-coloring of a map of the states of the United States (ignoring lakes).
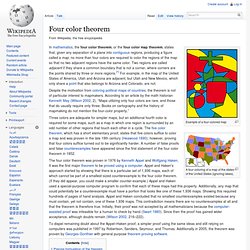
In mathematics, the four color theorem, or the four color map theorem, states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. Two regions are called adjacent if they share a common boundary that is not a corner, where corners are the points shared by three or more regions.[1] For example, in the map of the United States of America, Utah and Arizona are adjacent, but Utah and New Mexico, which only share a point that also belongs to Arizona and Colorado, are not.
Despite the motivation from coloring political maps of countries, the theorem is not of particular interest to mapmakers. The four color theorem was proven in 1976 by Kenneth Appel and Wolfgang Haken. Precise formulation of the theorem[edit] History[edit] 11/11/11 Palindrome Date | The Amazing Mathematics of Nov. 11, 2011 | Weird News. Today's date, 11/11/11, is a once-in-a-century occurrence, adding to a November has been a very fun month for recreational mathematicians. Last week, a rare eight-digit palindrome date — 11/02/2011, which reads the same frontward and backward — was found to have other mathematical qualities that made it a once-in-10,000-years date.
Aziz Inan, a professor of electrical engineering at the University of Portland, Oregon, crunched the numbers and found that when the date was expressed as a number, 11,022,011, it has very special properties. "It is the product of 7 squared times 11 cubed times 13 squared. That is impressive because those are three consecutive prime numbers. A once-in-10,000-years date is hard to top, but 11/11/11 is no slouch. After today, 11/11/11 will next occur 100 years down the road, on Nov. 11, 2111. Then, split 36 into three consecutive numbers that add up to 36 (11, 12 and 13).
Canal de Vihart. The simplest proof mathematicians needed two tries at. The most interesting mathematical mistake in the solar system. Scientists still puzzled by a fractal discovered 500 years ago. Mathematics as the raw material for art. Kat Austen, Culture Lab editor (Image: Hiroshi Sugimoto) In a new Paris exhibition, prizewinning mathematicians team up with artists to inspire works that bring intangible concepts to life Mathematics - A Beautiful Elsewhere, Fondation Cartier, Paris, until 18 March IF YOU think of cosmology, you picture colourful nebulae; with neurology, intricate brain scans.
But what does mathematics look like? That's what a team of world-class artists and mathematicians set out to discover. The product of the collaboration is the exhibition Mathematics - A Beautiful Elsewhere, at the Fondation Cartier in Paris, France. Ambitious perhaps, but the team has impressive credentials: the mathematical line-up boasts three Fields medal winners, including 2010 recipient Cédric Villani. Although some of the works might also fit well in a science museum, they are very much at home in the airy halls of one of Paris's premier contemporary art spaces. One example of artistic licence has made it into the show. Known Amicable Pairs. This is an attempt to collect all known amicable pairs. 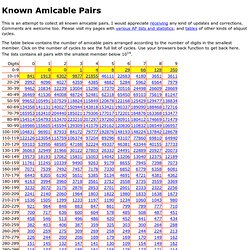I would appreciate receiving any kind of updates and corrections. Comments are welcome too. Please visit my pages with various AP lists and statistics; and tables of other kinds of aliquot cycles.
The table below contains the number of amicable pairs arranged according to the number of digits in the smallest member. Click on the number of cycles to see the full list of cycles. Update History: 28-Sep-2007 Now 11,994,387 pairs. 20-Nov-2006 Now 11,446,960 pairs. 05-Jun-2006 Now 11,222,079 pairs. 29-Dec-2005 Now 10,410,218 pairs. 04-Oct-2005 Major update -- now 10,306,909 pairs. Thanks to: Herman te Riele, David Moews, Mariano Garcia, David Einstein, Derek Ball, Frank Zweers, Yasutoshi Kohmoto, Patrick Costello, Stefan Battiato, Anatoly Gubanov, Andrew Walker, Walter Borho, Axel vom Stein, Sergey Chernych, Harvey Dubner, Paul Jobling, Sally Knight, Michel Marcus, Ren Yuanhua.
Last update: 28-Sep-2007. Math in a Minute: Welcome to Hotel Infinity paradox. A mathematical bug shows us why the 3D universe carries the possibility of despair. Really. For N bug-steps, there are two things to consider: how many total possible paths of N steps the bug has available to it, and how many of those N-step paths lead home. For example, let's look at 1D. After just 2 steps (N=2), where the bug could only go left or right each step, the bug has had 4 possible paths available to it: LR - Home RL - Home Of those, 2 lead home, giving it a home-probability of 50% after 2 steps.
Now let's look at 4 steps (still in 1D). The bug has now had 16 possible paths available to it: LLRR - Home LRLL - Home (earlier) LRLR - Home (twice) LRRL - Home (twice) LRRR - Home (earlier) RLLL - Home (earlier) RLLR - Home (twice) RLRL - Home (twice) RLRR - Home (earlier) RRLL - Home Out of 16 possible 4-step paths, 10 of them led back home. Now let's look at 2D, where the bug has 4 choices each step: up, down, left, or right. 4 steps leaves the bug with 256 possible paths, 84 of which lead home at either 2 or 4 steps.
That's why the bug isn't guaranteed to make it back in 3D. A mathematical bug shows us why the 3D universe leads to Murphy's Law. Let's also not forget that unlike, a path, the movement of any string no matter how thin is at least partially governed by the slight recoiling that occurs at the bends and curves. I think analogies are wonderful for explaining complex systems to simple folk like myself, but I hate it when "scientists" try to prove a mathematical system with an insufficient metaphor. Exactly what I was thinking. The way a string falls is not random. Even if you stood there shaking the box it still has all manner of constraints based on where parts of the string both forward and backward from each position are.
Like if you have a spiral, and you imagine this bugs walk is from the top spiralling down, this bug cannot actually walk directly downwards because another part of the spiral is already there, no matter how much you try to randomise it with shaking. Uncovering Da Vinci's Rule of the Trees. As trees shed their foliage this fall, they reveal a mysterious, nearly universal growth pattern first observed by Leonardo da Vinci 500 years ago: a simple yet startling relationship that always holds between the size of a tree's trunk and sizes of its branches.
A new paper has reignited the debate over why trees grow this way, asserting that they may be protecting themselves from wind damage. "Leonardo's rule is an amazing thing," said Kate McCulloh of Oregon State University, a scientist specializing in plant physiology. "Until recently, people really haven't tested it.
" Da Vinci wrote in his notebook that "all the branches of a tree at every stage of its height when put together are equal in thickness to the trunk. " To investigate why this rule may exist, physicist Christophe Eloy, from the University of Provence in France, designed trees with intricate branching patterns on a computer. Once the skeleton was completed, Eloy put it to the test in a virtual wind tunnel. The odd genius who showed that one infinity was greater than another. Ralph Abraham.