

Mathematiciens. Calculus: Differentials and integrals. Differentiation: How rapidly does something change?
The velocity is the rate of change of displacement. Let's look at a very simple case. The strange man in this animation is moving in a straight line at a constant speed of one metre per second. This means that, for each second he travels, his displacement from the starting position increases by 1 m. (An aside for physicists: velocity is a vector, meaning that it has direction as well as magnitude. When the clock strikes zero, he is at x = 3 m. When the clock reads t = 2 s, he is at x = 5 m. Now this is a special case, because in this example he is travelling at constant speed. , pronounced 'v bar'. Varying derivatives What if v is not constant? Analytical derivatives But what if we 'know' the formula for the function x(t)? Power terms and polynomials Let's have a look at these terms in turn. But what of a term like x = Ct2? Now let's make Δt and Δx extremely small, and we signify this by writing them as dt and dx.
Sums of terms The chain rule. Histoire des Mathématiques partie 2/2 - une vidéo High-tech et Science. Histoire des Mathématiques partie 1/2 - une vidéo High-tech et Science. Dimensions - Chapitre 4 - Français. Dimensions Chapitres 5 et 6. Deux notions seront utiles pour la suite : Le module d'un nombre complexe z= x +i y est simplement la distance du point correspondant (x,y) à l'origine.

On le note |z| et il est égal, d'après le théorème de Pythagore à √ (x2+y2) . Par exemple, le module de i est égal à 1 et celui de 1+i à √2. L'argument indique la direction de z. On le note Arg(z) et ce n'est rien d'autre que l'angle entre l'axe des abscisses et la droite joignant l'origine à (x,y). Les mathématiciens ont longtemps essayé de faire la même chose dans l'espace de dimension 3 : comment multiplier des points dans l'espace ? En résumé, les points du plan sont définis par un seul nombre... complexe. Vidéos mathématiques. Dimensions Chapitre 2. Dans le film, on voit les cinq polyèdres réguliers qui traversent le plan et on montre les sections/polygones qui se déforment.

Ce n'est pas facile car les sections dépendent de la manière dont les polyèdres traversent le plan. Par exemple, si un cube se présente de manière qu'une de ses faces soit parallèle au plan, il n'y a pas de surprise : les sections sont des carrés. Mais si on coupe un cube par un plan qui passe par son centre et qui est perpendiculaire à une diagonale, l'intersection est un... hexagone régulier et ceci est peut-être moins évident ?! Après avoir regardé tous les polyèdres traverser le plan, Escher vous propose des exercices.
Il vous montre les sections polygonales dans le plan et vous devez deviner le polyèdre qui est en train de traverser, comme si vous étiez un lézard plat. Nous pourrions faire la même chose et faire rouler les cinq polyèdres sur un plan et les projeter stéréographiquement. Des triangles, des gaz et des hommes - Cédric Villani - Université Nice Sophia Antipolis. Des particules, des étoiles et des probabilités. Ghys:poincaré. Bourguignon:perelman. Fourier. ▶ villani:poincaré. ▶ villani:chaos. Institut Henri Poincaré. L'Institut Henri Poincaré produit un documentaire exclusif de 32 minutes sur le mathématicien d'exception Joseph-Louis Lagrange, en coproduction avec le CNRS Images et en partenariat avec l'Institut Lagrange de Paris.Des historiens retracent le parcours européen de Lagrange et montrent comment il est passé d'académicien protégé des puissants à un professeur chargé d'éduquer les nouveaux Citoyens au moment de la Révolution Française.
Ils posent la question de l'implication des scientifiques dans la vie politique de l'époque. Des scientifiques expliquent combien les travaux de Lagrange, notamment en analyse et en mécanique céleste, sont novateurs dans la façon de concevoir les problèmes à l'époque, et permettent de comprendre comment il s'est positionné à la frontière entre les mathématiques et la physique, et a pu profondément marquer les sciences et leur enseignement jusqu'à aujourd'hui. Cédric Villani explique le Nombre d'or au Futuroscope. Cédric Villani : Les Fabuleux théorèmes de Nash. Tensor Calculus Lecture 0: Introduction. Fonction polynôme. Un article de Wikipédia, l'encyclopédie libre. ) de la forme : où est un entier naturel et sont des éléments de , appelés coefficients de la fonction polynôme .
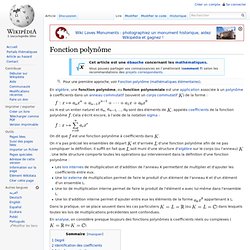
On dit que. Math - Matrix Algebra.