

Fourier series. In mathematics, a Fourier series (English pronunciation: /ˈfɔərieɪ/) decomposes periodic functions or periodic signals into the sum of a (possibly infinite) set of simple oscillating functions, namely sines and cosines (or complex exponentials).
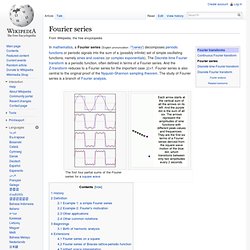
The Discrete-time Fourier transform is a periodic function, often defined in terms of a Fourier series. And the Z-transform reduces to a Fourier series for the important case |z|=1. Fourier series is also central to the original proof of the Nyquist–Shannon sampling theorem. The study of Fourier series is a branch of Fourier analysis. History[edit] The Fourier series is named in honour of Jean-Baptiste Joseph Fourier (1768–1830), who made important contributions to the study of trigonometric series, after preliminary investigations by Leonhard Euler, Jean le Rond d'Alembert, and Daniel Bernoulli.
The heat equation is a partial differential equation. Definition[edit] is a periodic function with period P. Where: approximates on Other applications[edit] Fourier analysis. Today, the subject of Fourier analysis encompasses a vast spectrum of mathematics.

In the sciences and engineering, the process of decomposing a function into simpler pieces is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. In mathematics, the term Fourier analysis often refers to the study of both operations. Applications[edit] Fourier analysis has many scientific applications – in physics, partial differential equations, number theory, combinatorics, signal processing, imaging, probability theory, statistics, option pricing, cryptography, numerical analysis, acoustics, oceanography, sonar, optics, diffraction, geometry, protein structure analysis and other areas.
This wide applicability stems from many useful properties of the transforms: Applications in signal processing[edit] Some examples include: Variants of Fourier analysis[edit] (Continuous) Fourier transform[edit] which is the inverse transform formula. Fourier transform. Definition[edit] There are several common conventions for defining the Fourier transform of an integrable function (Kaiser 1994, p. 29), (Rahman 2011, p. 11).
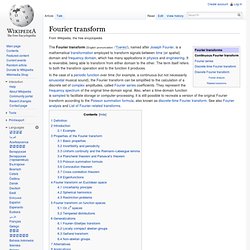
This article will use the following definition: , for any real number ξ. When the independent variable x represents time (with SI unit of seconds), the transform variable ξ represents frequency (in hertz). Is determined by via the inverse transform: , for any real number x. The statement that can be reconstructed from is known as the Fourier inversion theorem, and was first introduced in Fourier's Analytical Theory of Heat (Fourier 1822, p. 525), (Fourier & Freeman 1878, p. 408), although what would be considered a proof by modern standards was not given until much later (Titchmarsh 1948, p. 1).
And often are referred to as a Fourier integral pair or Fourier transform pair (Rahman 2011, p. 10). Introduction[edit] The Fourier transform relates the function's time domain, shown in red, to the function's frequency domain, shown in blue. Then If so. Fast Fourier transform. Frequency and time domain for the same signal A fast Fourier transform (FFT) is an algorithm to compute the discrete Fourier transform (DFT) and its inverse.
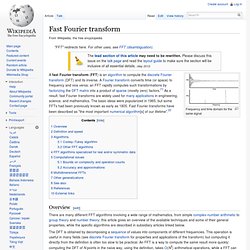
A Fourier transform converts time (or space) to frequency and vice versa; an FFT rapidly computes such transformations by factorizing the DFT matrix into a product of sparse (mostly zero) factors.[1] As a result, fast Fourier transforms are widely used for many applications in engineering, science, and mathematics. The basic ideas were popularized in 1965, but some FFTs had been previously known as early as 1805.
Fast Fourier transforms have been described as "the most important numerical algorithm[s] of our lifetime".[2] Overview[edit] The best-known FFT algorithms depend upon the factorization of N, but there are FFTs with O(N log N) complexity for all N, even for prime N. Is an N-th primitive root of unity, and thus can be applied to analogous transforms over any finite field, such as number-theoretic transforms. Algorithms[edit]