

Algorithms. New Tab. Colourings. What is a rhombille grid? A rhombille grid is a tessellation of the plain in identical rhombi.
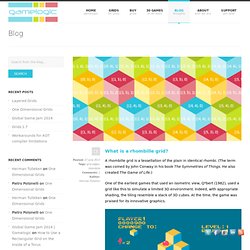
(The term was coined by John Conway in his book The Symmetries of Things. He also created The Game of Life.) One of the earliest games that used an isometric view, Q*bert (1982), used a grid like this to simulate a limited 3D environment. Indeed, with appropriate shading, the tiling resemble a stack of 3D cubes. At the time, the game was praised for its innovative graphics.
Another game that uses a rhombille grid is Rhomboid Slitherlinks, a set of puzzles created by Jim Bumgardner. The rombille grid has another feature that makes them useful for games. There are not many examples of games played on the edges of these types of grids. When you work with edges for hex or tri grids, there are several advantages to work with rhomb tiles instead of tris or hexes: It is easier to draw the edges, since you are not near the edge of the tile. Coordinates.
Grids. Alquerque and the checkered squareSinglegrid and doublegrid gamesThe hexgrid and its relation to the square gridThe checkered hexgrid - subgridsOne league beyond and one league behind Alquerque and the checkered square The draughts variants discussed here are played on boards with square or hexagonal grids.

The use of these grids has varied in time and place, the hexgrid being a very recent addition to an otherwise 'square' history. Rather than taking knowledge of the boards' properties for granted, we'll first discuss the basics here, not from a historical point of view, but from a topological one. Our point of departure is a regular square grid (1). It has squares and vertices. In (4) half the diagonals have been removed, in (6) half the straight lines, but topologically they are identical. The transfer from vertices to squares, according to the Dutch draughts historian Arie van der Stoep, occured in the 14th century: List of convex uniform tilings. This table shows the 11 convex uniform tilings (regular and semiregular) of the Euclidean plane , and their dual tilings.
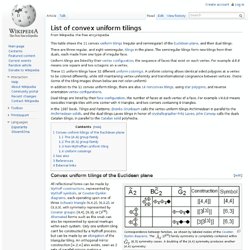
There are three regular, and eight semiregular, tilings in the plane. The semiregular tilings form new tilings from their duals, each made from one type of irregular face. Uniform tilings are listed by their vertex configuration , the sequence of faces that exist on each vertex. For example means one square and two octagons on a vertex. These 11 uniform tilings have 32 different . In addition to the 11 convex uniform tilings, there are also 14 nonconvex tilings , using star polygons , and reverse orientation vertex configurations .
Dual tilings are listed by their face configuration , the number of faces at each vertex of a face. Rhombille tiling. In geometry, the rhombille tiling,[1] also known as tumbling blocks,[2] reversible cubes, or the dice lattice, is a tessellation of identical 60° rhombi on the Euclidean plane.
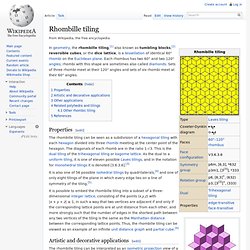
Each rhombus has two 60° and two 120° angles; rhombi with this shape are sometimes also called diamonds. Sets of three rhombi meet at their 120° angles and sets of six rhombi meet at their 60° angles. Properties[edit]
Amit’s Thoughts on Grids. Grids are commonly used in games for representing playing areas such as maps (in games like Civilization and Warcraft), playing surfaces (in games like pool, table tennis, and poker), playing fields (in games like baseball and football), boards (in games like Chess, Monopoly, and Connect Four), and abstract spaces (in games like Tetris).
I’ve attempted to collect my thoughts on grids here on these pages. I avoid implementation details (such as source code) and instead focus on concepts and algorithms. I’ve mostly used grids to represent maps in strategy and simulation games. Although many of the concepts here are useful for all sorts of grids, there is a bias towards the kinds of games I am interested in.
Grids are built from a repetition of simple shapes. Squares Figure 1: Square Grid The most common grid is a square grid. Hexagons Figure 2: Hexagon Grid Hexagons have been used in some board and computer games because they offer less distortion of distances than square grids. Triangles.