

Why is this Puzzle Impossible? - Numberphile. What are the chances of a class with 24 students having 3 pairs of students sharing a birthday? – Mike's Math Page. A Country Seeking Males (puzzle) Today re-running another favorite puzzle, from 6 years ago.
I took it from Richard Wiseman who stated it this way: "Imagine there is a country with a lot of people. These people do not die, the people consists of monogamous families only, and there is no limit to the maximum amount of children each family can have. 7 Vs 11 Sided Dice Game: Can You Solve It? In front of you are two fair dice.

One is a 7-sided dice with faces -3, -2, -1, 0, 1, 2, 3. The other is an 11-sided dice with faces -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5. You pick a dice, and I will get the other one. We will roll together, and the person with the larger number wins. If the two dice show the same number, we roll again until someone wins. Which dice should you pick, if you want to maximize your chance of winning? Simulating simple dice games. A necessary but not sufficient condition for a game being one of skill rather than pure chance is that the player gets to make choices.
If the game play is fully automatic, as in standard Snakes and Ladders, then there cannot possibly be any skill involved. However, any game of pure chance can be converted to one of skill simply by adding a wager, or similar tool that sets up decisions for players such as the doubling cube in backgammon (backgammon of course is not a game of pure chance even just in the checker play, but it’s the doubling cube that brings in most of the skill). This is one of the reasons why so much effort over the centuries has gone into understand the probabilities of elementary card and dice games; leveraging the probabilities into a gamble turn a game of low or zero skill into something much more interesting. Note - if you’re reading this on R Bloggers, the graphics aren’t showing up for a reason I need time to troubleshoot. Can You Solve The Cats And Random Mouse Riddle? There are 7 doors in a line.

A mouse starts in the middle at door 4. At doors 1 and 7 are cats. Can You Solve The Chess Match Riddle? Pr(Win Two In A Row) = ? Thanks to Mika from Sweden for suggesting this problem!

Can You Solve The Cats And Random Mouse Riddle? Μαθη...μαγικα: Σημεία. Tricky Apple Tree Probability Problem From The Online Math Olympiad. I was suggested this problem by Arbitrary Renaissance who credits the Online Math Olympiad (OMO).
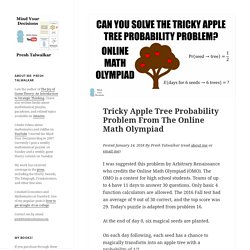
The OMO is a contest for high school students. Teams of up to 4 have 11 days to answer 30 questions. Only basic 4 function calculators are allowed. The 2016 Fall test had an average of 9 out of 30 correct, and the top score was 29. Today’s puzzle is adapted from problem 16. At the end of day 0, six magical seeds are planted. On each day following, each seed has a chance to magically transform into an apple tree with a probability of 1/2. Once a seed transforms into an apple tree, it stays an apple tree and survives indefinitely. What is the expected number of days until all six seeds have become apple trees? Sharing Nassim Taleb’s dart probability problem with kids. Last week Nassim Taleb posted a fun probability problem on Twitter: I “live blogged” my work on this problem at the link below and eventually found the solution (though after a long detour): Sort of live blogging a solution to a problem posed by Nassim Taleb One of the boys had to leave early this morning for a school event, so I was looking for a quick project.
With some of the work I did in Mathematica on Taleb’s problem still up on my computer screen, I decided to run through the problem with the boys. The point here wasn’t for them to figure out the solution, but rather to see a neat example of counting techniques used to solve a challenging problem. Programmer Interview Question – The Probability Of Adjacent Seating – Mind Your Decisions. 5 people (a, b, c, d, e) are seated randomly around a circular table.

What is the probability a and b will be seated next to each other? What is the probability, if they are seated randomly in a row? What is the probability if there are n people seated randomly? Solve for random seating around a circular table and in a row. (Seated randomly means the uniform distribution–each person is equally likely to be in any seat). This problem has been asked as an interview question for programmers. Can You Solve The Code Lock Puzzle? Sunday Puzzle – Mind Your Decisions. I got this interesting puzzle by email.

A safe has a code lock that unlocks if you input the correct four digits, in any order. The lock has a keypad the digits 0, 1, 2, …, 9. For example, suppose the unlock code is 1000. How Many Friends You Need to Have a Birthday Every Day of the Year. It seems like every day I log in to Facebook, it’s someone’s birthday, and I’m not even a very active user.

I think it’s been at least a year since I last friended someone. Maybe two. Also, I have fewer than 365 friends on the social network, so it’s mathematically impossible for there to be a birthday every single day of the year. But still, it seems like a lot of days with at least one birthday. Two questions: How many friends do you need to nearly guarantee that during any given day of the year, it’s at least one friend’s birthday? I was sure someone had answered these question before, so I googled it first. More generally, in probability theory, this is known as the coupon collector’s problem. Here’s what the probabilities look like, as it pertains to our birthday problem. The Loaded Dice Puzzle. And My Reaction to Power-Up, A New Book – Mind Your Decisions. A standard dice shows the number 6, and every number, with probability 1/6.
The dice is modified so the number 6 appears half as often as the other numbers. What probability of rolling a 6 on the new dice? (Clarification per comment from blink: “half as often as each of the other numbers”) Decisionsciencenews. Main TWO SHOT RUSSIAN ROULETTE WITH 2 BULLETS OR AN EQUAL CHANCE OF 1 or 3 BULLETS With p as the probability of dying on one shot, this figure shows how to get the probability of living through the game. Peter Ayton is giving a talk today at the London Judgement and Decision Making Seminar Imagine being obliged to play Russian roulette – twice (if you are lucky enough to survive the first game).
A recipe for dynamic programming in R: Solving a “quadruel” case from PuzzlOR – Serhat's Blog. As also described in Cormen, et al (2009) p. 65, in algorithm design, divide-and-conquer paradigm incorporates a recursive approach in which the main problem is: Divided into smaller sub-problems (divide),The sub-problems are solved (conquer),And the solutions to sub-problems are combined to solve the original and “bigger” problem (combine). Instead of constructing indefinite number of nested loops destroying the readability of the code and the performance of execution, the “recursive” way utilizes just one block of code which calls itself (hence the term “recursive”) for the smaller problem. The main point is to define a “stop” rule, so that the function does not sink into an infinite recursion depth.
Book Proofs – A blog for mathematical riddles, puzzles, and elegant proofs. This Riddler puzzle is about a card game where the goal is to find the largest card. Approximate solution Let’s suppose that the deck has nn cards in it, and we are dealt kk cards from the deck. Every time a card is flipped, we must decide whether to keep playing or to stop. Suppose we have flipped over mm cards already and the largest card flipped so far has a value of aa. Some quick observations: If the last card we flipped has value smaller than aa, then we must clearly keep flipping cards, for we would definitely lose if we stopped playing now. Can You Solve The Probability Two Random Walkers Meet? A Strange Way To Approximate Pi. Sunday Puzzle – Mind Your Decisions. 40 Questions on Probability for data science - [Solution: SkillPower - Probability, DataFest 2017] Introduction Probability forms the backbone of many important data science concepts from inferential statistics to Bayesian networks.
It would not be wrong to say that the journey of mastering statistics begins with probability. What Is The Probability It Will Rain Forever? Sunday Puzzle – Mind Your Decisions. Weather in Mathland is determined by chance. The Missing Sock Problem – Sunday Puzzle – Mind Your Decisions. Can You Solve The Probability The Newborn Is A Boy? Technical Interview Question – Sunday Puzzle – Mind Your Decisions. On the morning of January 1, a hospital nursery has 3 boys and some number of girls. Can You Solve Google’s Car Probability Interview Question? Sunday Puzzle – Mind Your Decisions. The Race To December 31 – Sunday Puzzle – Mind Your Decisions. Here’s a fun game you can play with another person. Διασκεδαστικά Μαθηματικά: Κοινοβουλευτική πρακτική. Διασκεδαστικά Μαθηματικά: Λύτες προβλημάτων. Distance Between Two Random Points In A Square – Sunday Puzzle – Mind Your Decisions.
Μισθολογικές ανισότητες. Michael Fenton’s counting problem. Another riddle. A very nice puzzle on The Riddler last week that kept me busy on train and plane rides, runs and even in between over the weekend. Διασκεδαστικά Μαθηματικά: Το δείπνο του κ. Καθηγητή ( Rolling Dice ( When Warren Buffett Challenged Bill Gates To A Dice Game – Sunday Puzzle – Mind Your Decisions. Number Of Ways To Divide Coins Interview Question – Sunday Puzzle – Mind Your Decisions. Combinatorics Problem on Geometric Distribution: Can You Roll The Die? - Soumik Chakraborty. Διασκεδαστικά Μαθηματικά: Αναλογικό ρολόι. Odd Numbers in Pascal's Triangle. Secret Santa Surprising Probability – Sunday Puzzle. Οι Τρόποι.
Library(e1071) library(dplyr) c("A1","A2","A3","C1","C2") %>% length %>% permutations %>% data.frame %>% mutate_each(funs(x[.])) %>% filter (!X1 %in% c("A3","C1","C2")) %>% filter (!X2 %in% c("C1","C2")) – gd047
How Many 3×3 Magic Squares Are There? Sunday Puzzle. Dice rolls until a repeat – Sunday Puzzle. Διασκεδαστικά Μαθηματικά: Διαδρομές. Διασκεδαστικά Μαθηματικά: 5 πριν το 7. Βάτραχος vs ...μύγες. Πιθανότητες και Ιατρική. Ψαρομεζές. 7 ντόμινο. Νο $123456789$ Πεντάγωνο νησί. To Pizza or not to Pizza? Solutions to knight's random walk. Πρώτο ποιο; Ουρά...... 8 - ψήφιοι αριθμοί. Χρόνος ζωής. Ασκήσεις ιστορικού ενδιαφέροντος - Πιθανότητες (6) Τρία κουτιά. Το πρόβληµα του σπιρτόκουτου του Banach. ▪ Τεσσάρι στο ΛΟΤΤΟ. ▪ 365 άτομα. 5 για 2 και 2 για 5.