

Epistemic, ontological and aleatory risk « Critical Uncertainties. What do an eighteenth century mathematician and a twentieth century US Secretary of Defence have to do with engineering and risk?
The answer is that both thought about uncertainty and risk, and the differing definitions that they arrived at neatly illustrate that there is more to the concept of risk than just likelihood multiplied by consequence. Which in turn has significant implications for engineering risk management. Editorial note. I’ve pretty much completely revised this post since the original, hope you like it The concept of risk allows us to make decisions in an uncertain world where we cannot perfectly predict future outcomes. Which leads us to the point that Secretary Rumsfeld was making, that uncertainty is a continuum that ranges from that which we are certain of at one end through to that which we are completely ignorant of at the other. Why risk community rejects science, logic and common sense RISK-ACADEMY Blog.
First, I wanted to share an extract from the book I am reading at the moment Alchemy: The Dark Art and Curious Science of Creating Magic in Brands, Business, and Life The chapter is called “I Know It Works in Practice, but Does It Work in Theory?

On John Harrison, Semmelweis and the Electronic Cigarette” and I though it gives a great historical take on why most risk managers and all risk management associations reject decision science, probability theory and neuroscience. Here is the quote from the chapter: In a sensible world, the only thing that would matter would be solving a problem by whatever means work best, but problem-solving is a strangely status-conscious job: there are high-status approaches and low-status approaches.
But compared to an eighteenth-century counterpart, Jobs had it easy. Alongside Harrison’s remarkable technological work, there is also an interesting psychological aspect to this story. Check out other decision making books. ""project risk management"" on SlidePlayer. Managing risk in organisations – Broadleaf. Free courseware on risk engineering and safety management. PM/U4 Topic 5 Steps in Risk Management – theintactone.com.
All risk management processes follow the same basic steps, although sometimes different jargon is used to describe these steps.

Together these 5 risk management process steps combine to deliver a simple and effective risk management process. Step 1: Identify the Risk You and your team uncover, recognize and describe risks that might affect your project or its outcomes. There are a number of techniques you can use to find project risks. During this step you start to prepare your Project Risk Register. Risk Assessment. Fondation pour une Culture de Sécurité Industrielle — Foncsi. Epistemic, ontological and aleatory risk « Critical Uncertainties. ISO 31000 Risk Management Definitions in Plain English. SHARE TO SUCCESS - DOCSLIDE.COM.BR. Cox’s risk matrix theorem and its implications for project risk management. Introduction One of the standard ways of characterising risk on projects is to use matrices which categorise risks by impact and probability of occurrence.

These matrices provide a qualitative risk ranking in categories such as high, medium and low (or colour: red, yellow and green). Such rankings are often used to prioritise and allocate resources to manage risks. There is a widespread belief that the qualitative ranking provided by matrices reflects an underlying quantitative ranking. In a paper entitled, What’s wrong with risk matrices? Since the content of this post may seem overly academic to some of my readers, I think it is worth clarifying why I believe an understanding of Cox’s principles is important for project managers. Background and preliminaries Let’s begin with some terminology that’s well known to most project managers: Probability: This is the likelihood that a risk will occur. Impact (termed “consequence” in the paper): This is the severity of the risk should it occur. Quantification of margins and uncertainties. Quantification of Margins and Uncertainty (QMU) is a decision-support methodology for complex technical decisions.
QMU focuses on the identification, characterization, and analysis of performance thresholds and their associated margins for engineering systems that are evaluated under conditions of uncertainty, particularly when portions of those results are generated using computational modeling and simulation.[1] QMU has traditionally been applied to complex systems where comprehensive experimental test data is not readily available and cannot be easily generated for either end-to-end system execution or for specific subsystems of interest. Examples of systems where QMU has been applied include nuclear weapons performance, qualification, and stockpile assessment.
QMU focuses on characterizing in detail the various sources of uncertainty that exist in a model, thus allowing the uncertainty in the system response output variables to be well quantified. History[edit] Overview[edit] Quantification of margins and uncertainties. Fuzzy logic. Fuzzy logic is a form of many-valued logic in which the truth values of variables may be any real number between 0 and 1.
It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false.[1] By contrast, in Boolean logic, the truth values of variables may only be the integer values 0 or 1. The term fuzzy logic was introduced with the 1965 proposal of fuzzy set theory by Lotfi Zadeh.[2][3] Fuzzy logic had however been studied since the 1920s, as infinite-valued logic—notably by Łukasiewicz and Tarski.[4] Fuzzy logic has been applied to many fields, from control theory to artificial intelligence.
Overview[edit] Classical logic only permits conclusions which are either true or false. Knowledge Base. Knowledge database All Whitepapers Webinars Case studies All ModelRisk Tamara StopRisk Pelican Training Consulting Custom software.
Epistemic, ontological and aleatory risk « Critical Uncertainties. Home - Risk IQ. SCRAM. NCCA. Norman Fenton homepage. Director of Risk Information Management Research Group School of Electronic Engineering and Computer Science Queen Mary University of London London E1 4NS. n.fenton at qmul.ac.uk Tel +44 20 7882 7860 Agena Ltd, 11 Main Street, Caldecote Cambridge CB23 7NU Tel: + 44 (0) 1223 263880 www.agenarisk.com norman at agena.co.uk.

Simple Online Collaboration: Online File Storage, FTP Replacement, Team Workspaces. Probabilistic Project Management at NASA with Joint Confidence Level (JCL-PC) On the Strategic Project and Portfolio Management Blog by Simon Moore one can find many fascinating stories about project failures as well as a related collection of project management case studies.
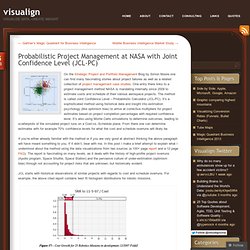
One entry there links to a project management method NASA is mandating internally since 2009 to estimate costs and schedule of their various aerospace projects. The method is called Joint Confidence Level – Probabilistic Calculator (JCL-PC). It’s a sophisticated method using historical data and insight into estimation psychology (like optimism bias) to arrive at corrective multipliers for project estimates based on project completion percentages with required confidence level.
It’s also using Monte Carlo simulations to determine outcomes, leading to scatterplots of the simulated project runs on a Cost-vs. -Schedule plane. If you’re either already familiar with the method or if you are very good at abstract thinking the above paragraph will have meant something to you. Uncertainty quantification.
Uncertainty quantification (UQ) is the science of quantitative characterization and reduction of uncertainties in applications.
It tries to determine how likely certain outcomes are if some aspects of the system are not exactly known. An example would be to predict the acceleration of a human body in a head-on crash with another car: even if we exactly knew the speed, small differences in the manufacturing of individual cars, how tightly every bolt has been tightened, etc., will lead to different results that can only be predicted in a statistical sense. Concept Symposia on Project Governance. Www.pwrengineering.com/systems/images/Linking_RM_to_PM.pdf. Www.rocketdynetech.com/dataresources/RiskAndOpportunityManagement-ProgramAndProjectManagementSuccessFactors.pdf.