

Simple Mathematics Component with C#, VB. (20) Computing a tangent plane. 3Blue1Brown. ProArchitect #007 - Voronax - Structural Engineering inspired by Nature. Advances in Architectural Geometry 2018. Minimal Surfaces. Computational Design – Computer Graphics and Geometry Laboratory. Open Positions – Computer Graphics and Geometry Laboratory. We are currently looking for Ph.D. students in the general area of geometric computing with a focus on smart materials, complex assemblies, computational caustics, and computational design.
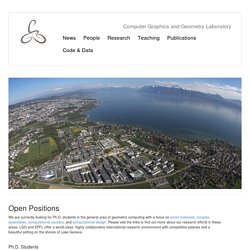
Please visit the links to find out more about our research efforts in these areas. LGG and EPFL offer a world-class, highly collaborative international research environment with competitive salaries and a beautiful setting on the shores of Lake Geneva. Ph.D. Students Applicants should have a 4-5 year bachelor's degree or a master's degree in computer science, math, engineering, or related fields.
Potential PhD Topics Complex Assemblies 3D assemblies refer to objects that combine multiple component parts into a structure with a specific form and/or functionality. Keywords: combinatorial optimization, graph algorithms, geometry optimization, joining technology, robotic assembly More information Smart Materials. Computer Graphics and Geometry Laboratory. Interactive Design Exploration for Constrained Meshes. Computer-Aided Design 61: 13–23, 2015 Abstract In architectural design, surface shapes are commonly subject to geometric constraints imposed by material, fabrication or assembly.
Rationalization algorithms can convert a freeform design into a form feasible for production, but often require design modifications that might not comply with the design intent. In addition, they only offer limited support for exploring alternative feasible shapes, due to the high complexity of the optimization algorithm. Realtime Deformation of Constrained Meshes Using GPU. In GPU Computing and Applications, pp. 15-34.
Springer Singapore, 2015 Abstract Constrained meshes play an important role in freeform architectural design, as they can represent panel layouts on freeform surfaces. It is challenging to perform realtime manipulation on such meshes, because all constraints need to be respected during the deformation while the shape quality needs to be maintained. This usually leads to nonlinear constrained optimization problems, which are challenging to solve in real time. 3D-DREAMING "Architecture from a digital point of view".
OpenGL SuperBible Home PageOpenGL SuperBible. PyOpenGL Installation. Most users of PyOpenGL should use pip to install PyOpenGL automatically.
It can be installed either to the system Python or a Virtualenv. $ pip install PyOpenGL PyOpenGL_accelerate Manual Installation If you cannot, or would prefer not to, use pip, you can download the package from PyPI. The package uses Setuptools for its installation. $ tar -zxvf PyOpenGL-3.1.0.tar.gz $ cd PyOpenGL-3.1.0 $ python setup.py install.
Curvas y superficies en el diseño geométrico asistido por ordenador. El diseño geométrico asistido por ordenador tiene su origen esencialmente en la industria del automóvil.
El problema fundamental del que se ocupa consiste en describir las formas, curvas, superficies de un objeto (una pieza de una máquina, el casco de un buque o de un avión...) en forma matemática sencilla, pero eficiente y precisa, que permita trasladar a las oficinas técnicas las características del objeto para su manufactura. Curvas y Superficies en el Diseño Geométrico Asistido por Ordenador. Profesor de la asignatura: Leonardo Fernández JambrinaDirección: E.T.S.I.

Math. Teaching Computational Geometry and Topology. The Computational Geometry Algorithms Library. Computational Geometry. Shape Interrogation for Computer Aided Design and Manufacturing (Hyperbook Edition) To display this page you need a browser with JavaScript support.

Next: Preface Contents Index Nicholas M. Patrikalakis Takashi Maekawa Wonjoon Cho PrefaceContents1. OpenMesh. What is OpenMesh?

OpenMesh is a generic and efficient data structure for representing and manipulating polygonal meshes. OpenMesh is developed at the Computer Graphics Group, RWTH Aachen. It was funded by the German Ministry for Research and Education ( BMBF). It was designed with the following goals in mind: CS 294-1: Mesh Generation and Geometry Processing. This class is for computer graphics students who use triangle meshes, engineers and scientists who want to generate unstructured meshes for the finite element method or for manufacturing, and students of GIS (geographical information systems) who work with TINs (triangulated irregular networks).

It will be accessible to students in engineering and the sciences, as well as in computer science. The only prerequisite is a thorough familiarity with fundamental data structures (CS 61B or the equivalent). Releases · meshmash/Plankton. Mesh Subdivision: Loop and Catmull-Clark – bespoke geometry. Computational designers who work with meshes in Rhino + Grasshopper will inevitably be familiar with Giulio Piacentino’s brilliant Weaverbird plug-in.

It provides a great variety of outstanding tools for creating, managing and subdividing meshes. Using mesh subdivision and smoothing approaches allows for designers to start from coarse geometries and then rapidly transform them into fluid and organic shapes. However, Weaverbird’s implementations of the Loop and Catmull-Clark subdivision algorithms – two of the most standard methods for these approaches – lack some desirable features, specifically the ability for users to designate anchors and creases within the mesh. Mesh Subdivision: Loop and Catmull-Clark – bespoke geometry.
Non-uniform rational B-spline. In general, editing NURBS curves and surfaces is highly intuitive and predictable. Control points are always either connected directly to the curve/surface, or act as if they were connected by a rubber band. Depending on the type of user interface, editing can be realized via an element’s control points, which are most obvious and common for Bézier curves, or via higher level tools such as spline modeling or hierarchical editing. Historical background[edit] As computers were introduced into the design process, the physical properties of such splines were investigated so that they could be modelled with mathematical precision and reproduced where needed.
Pioneering work was done in France by Renault engineer Pierre Bézier, and Citroën's physicist and mathematician Paul de Casteljau. At first NURBS were only used in the proprietary CAD packages of car companies. Continuity[edit] Positional continuity (G0) holds whenever the end positions of two curves or surfaces coincide. Order[edit] . . Rhinoceros - NURBS. NURBS, Non-Uniform Rational B-Splines, are mathematical representations of 3‑D geometry that can accurately describe any shape from a simple 2‑D line, circle, arc, or curve to the most complex 3‑D organic free-form surface or solid.
Because of their flexibility and accuracy, NURBS models can be used in any process from illustration and animation to manufacturing. NURBS geometry has five important qualities that make it an ideal choice for computer-aided modeling. Several industry‑standard methods are used to exchange NURBS geometry. This means that customers are able to move their valuable geometric models between various modeling, rendering, animation, and engineering analysis programs. They can store geometric information in a way that will be usable for the foreseeable future. Non-uniform rational B-spline. Math.
Polar and Cartesian Coordinates. Non-uniform rational B-spline. Cwant/tessagon: Tessellate your favorite 2D manifolds with triangles, hexagons, and other interesting patterns. Amazon.
Essential Mathematics for Computational Design with C#, Python, VB. Shape Interrogation for Computer Aided Design and Manufacturing (Hyperbook Edition) Computational Geometry. Curves and Surfaces for CAGD, Fifth Edition: A Practical Guide (The Morgan Kaufmann Series in Computer Graphics): Gerald Farin: 9781558607378: Amazon.com: Books. Finding an Angle in a Right Angled Triangle. Angle from Any Two Sides We can find an unknown angle in a right-angled triangle, as long as we know the lengths of two of its sides. Example The ladder leans against a wall as shown. What is the angle between the ladder and the wall? The answer is to use Sine, Cosine or Tangent! But which one to use?
Step 1: find the names of the two sides we know Adjacent is adjacent to the angle, Opposite is opposite the angle, and the longest side is the Hypotenuse. Example: in our ladder example we know the length of: the side Opposite the angle "x", which is 2.5 the longest side, called the Hypotenuse, which is 5.