

Riemann sphere. The Riemann sphere can be visualized as the complex number plane wrapped around a sphere (by some form of stereographic projection – details are given below).
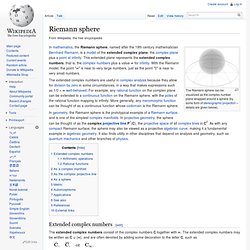
In mathematics, the Riemann sphere, named after the 19th century mathematician Bernhard Riemann, is a model of the extended complex plane, the complex plane plus a point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value ∞ for infinity. With the Riemann model, the point "∞" is near to very large numbers, just as the point "0" is near to very small numbers. In geometry, the Riemann sphere is the prototypical example of a Riemann surface, and is one of the simplest complex manifolds. In projective geometry, the sphere can be thought of as the complex projective line P1(C), the projective space of all complex lines in C2. Extended complex numbers[edit] The extended complex numbers consist of the complex numbers C together with ∞. Arithmetic operations[edit] Metric[edit] Möbius transformation. In geometry and complex analysis, a Möbius transformation of the plane is a rational function of the form of one complex variable z; here the coefficients a, b, c, d are complex numbers satisfying ad − bc ≠ 0.
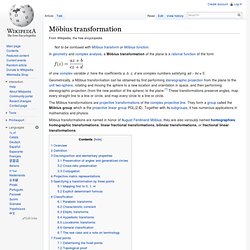
Geometrically, a Möbius transformation can be obtained by first performing stereographic projection from the plane to the unit two-sphere, rotating and moving the sphere to a new location and orientation in space, and then performing stereographic projection (from the new position of the sphere) to the plane.[1] These transformations preserve angles, map every straight line to a line or circle, and map every circle to a line or circle.
Möbius transformations are named in honor of August Ferdinand Möbius; they are also variously named homographies, homographic transformations, linear fractional transformations, bilinear transformations, or fractional linear transformations. Overview[edit] Möbius transformations are defined on the extended complex plane . Definition[edit] is with matrix If. Complex projective space. In mathematics, complex projective space is the projective space with respect to the field of complex numbers.
By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines through the origin of a complex Euclidean space (see below for an intuitive account). Formally, a complex projective space is the space of complex lines through the origin of an (n+1)-dimensional complex vector space. The space is denoted variously as P(Cn+1), Pn(C) or CPn. When n = 1, the complex projective space CP1 is the Riemann sphere, and when n = 2, CP2 is the complex projective plane (see there for a more elementary discussion). Complex projective space was first introduced by von Staudt (1860) as an instance of what was then known as the "geometry of position", a notion originally due to Lazare Carnot, a kind of synthetic geometry that included other projective geometries as well. . .
Inversive ring geometry. Duality (mathematics) In mathematical contexts, duality has numerous meanings[1] although it is "a very pervasive and important concept in (modern) mathematics"[2] and "an important general theme that has manifestations in almost every area of mathematics.
"[3] Duality can also be seen as a functor, at least in the realm of vector spaces. There it is allowed to assign to each space its dual space and the pullback construction allows to assign for each arrow f: V → W, its dual f∗: W∗ → V∗. the subset and superset relations ⊂ and ⊃ on any collection of sets,the divides and multiple-of relations on the integers, andthe descendant-of and ancestor-of relations on the set of humans.
A particular order reversal of this type occurs in the family of all subsets of some set S: if denotes the complement set, then A ⊂ B if and only if . According to Artstein-Avidan and Milman,[5][6] a duality transform is just an involutive antiautomorphism of a partially ordered set S, that is, an order-reversing involution.