

Borromean rings. Mathematical properties[edit] Although the typical picture of the Borromean rings (above right picture) may lead one to think the link can be formed from geometrically ideal circles, they cannot be.
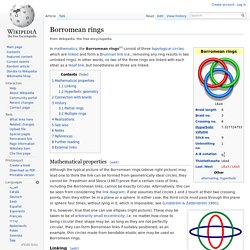
Freedman and Skora (1987) prove that a certain class of links, including the Borromean links, cannot be exactly circular. Alternatively, this can be seen from considering the link diagram: if one assumes that circles 1 and 2 touch at their two crossing points, then they either lie in a plane or a sphere. In either case, the third circle must pass through this plane or sphere four times, without lying in it, which is impossible; see (Lindström & Zetterström 1991). Geometric Topology. This area of mathematics is about the assignment of geometric structures to topological spaces, so that they "look like" geometric spaces.

For instance, compact two dimensional surfaces can have a local geometry based on the sphere (the sphere itself, and the projective plane), based on the Euclidean plane (the torus and the Klein bottle), or based on the hyperbolic plane (all other surfaces). Similar questions in three dimensions have more complicated answers; Thurston showed that there are eight possible geometries, and conjectured that all 3-manifolds can be split into pieces having these geometries.
Computer solution of these questions by programs like SnapPea has proved very useful in the study of knot theory and other topological problems. Acme Klein Bottle. A topologist's delight, handcrafted in glass. Poincaré conjecture. By contrast, neither of the two colored loops on this torus can be continuously tightened to a point.
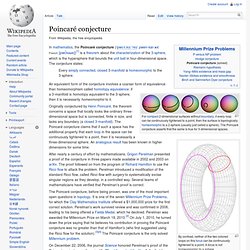
A torus is not homeomorphic to a sphere. Every simply connected, closed 3-manifold is homeomorphic to the 3-sphere. An equivalent form of the conjecture involves a coarser form of equivalence than homeomorphism called homotopy equivalence: if a 3-manifold is homotopy equivalent to the 3-sphere, then it is necessarily homeomorphic to it. The Poincaré conjecture, before being proven, was one of the most important open questions in topology. It is one of the seven Millennium Prize Problems, for which the Clay Mathematics Institute offered a $1,000,000 prize for the first correct solution.
History[edit] Poincaré's question[edit] At the beginning of the 20th century, Henri Poincaré was working on the foundations of topology—what would later be called combinatorial topology and then algebraic topology. The original phrasing was as follows: Attempted solutions[edit] 4-manifold. In mathematics, 4-manifold is a 4-dimensional topological manifold.

A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different. There exist some topological 4-manifolds which admit no smooth structure and even if there exists a smooth structure it need not be unique (i.e. there are smooth 4-manifolds which are homeomorphic but not diffeomorphic). 4-manifolds are of importance in physics because, in General Relativity, spacetime is modeled as a pseudo-Riemannian 4-manifold.
3-sphere. Definition[edit] In coordinates, a 3-sphere with center (C0, C1, C2, C3) and radius r is the set of all points (x0, x1, x2, x3) in real, 4-dimensional space (R4) such that The 3-sphere centered at the origin with radius 1 is called the unit 3-sphere and is usually denoted S3: It is often convenient to regard R4 as the space with 2 complex dimensions (C2) or the quaternions (H).
Möbius strip. A Möbius strip made with a piece of paper and tape.
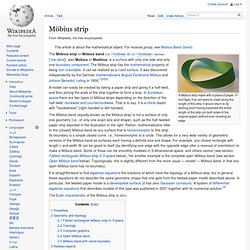
If an ant were to crawl along the length of this strip, it would return to its starting point having traversed the entire length of the strip (on both sides of the original paper) without ever crossing an edge. The Möbius strip or Möbius band (UK /ˈmɜrbiəs/ or US /ˈmoʊbiəs/; German: [ˈmøːbi̯ʊs]), also Mobius or Moebius, is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable.
It can be realized as a ruled surface. It was discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in 1858.[1][2][3] Klein bottle. Boy's surface. An animation of Boy's surface Boy's surface is discussed (and illustrated) in Jean-Pierre Petit's Le Topologicon.[1] Boy's surface was first parametrized explicitly by Bernard Morin in 1978.
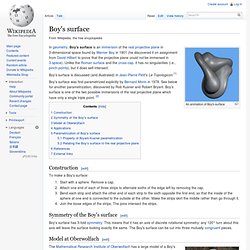
See below for another parametrization, discovered by Rob Kusner and Robert Bryant. Boy's surface is one of the two possible immersions of the real projective plane which have only a single triple point. [2] Construction[edit] To make a Boy's surface: