

Le nombre d’or dans la nature. La Pomme de Pin La pomme de pin montre clairement les spirales de Fibonacci : 8 vertes dans un sens, 13 rouges dans l'autre sens. 8 et 13 sont deux termes consécutifs de la suite de Fibonacci : 1; 1; 2; 3; 5; 8; 13.

Ses écailles sont alignées selon la spirale de Fibonacci : on représente les 4 coins des écailles de la pomme de pin par des points. Lorsqu'on relie ces points, on obtient des spirales qui tournent vers la droite, et d'autres vers la gauche. Ø le nombre de spirales vers la gauche et vers la droite sont deux nombres consécutifs de la suite de Fibonacci.
Ø chaque point appartient à deux spirales. Ø Lorsque l'on rejoint tous les points par une seule spirale, l'angle entre deux points consécutifs est l'angle d’or Cet emplacement en spirale se retrouve fréquemment dans la nature, notamment avec les plantes spiralées, comme par exemple les graines de tournesol, l'écorce d'ananas ou le coeur d'une marguerite. b) - le règne animal et l’homme. Le nombre d'or. SommairePartie I : Définition du nombre d'or Définition artistique Définition mathématique Calcul du nombre d'or Autres figuresPartie II : Le nombre d'or, un nombre d'art Comment font les artistes ?

Le nombre d'or. Mathématiques. Nombre_or.pdf (Objet application/pdf) Phi - Le Nombre d'Or - La Divine Porportion - l'ADN Divin. Les Romains, les Grecs, les Juifs et les Egyptiens semblaient tous d'accord : 1,618 était le nombre d'or, le nombre de l'harmonie universelle, le nombre de la création, le nombre de Dieu, le Créateur.

Lle nombre utilisé partout dans l'ordre caché de la Création et qu'il fallait donc employer dans les édifices dédiés au Créateur afin de s'en rapprocher. Empreint de mystère, objet d'un culte tantôt religieux, tantôt magique, le nombre d'or influence la vision occidentale de l'harmonie. Chez les Grecs, avec le développement de la géométrie, la secte secrète des pythagoriciens en avait fait un symbole d'harmonie universelle, de vie, d'amour et de beauté. Au Moyen-Age, les savants, les pères de l'église, les bâtisseurs, les maîtres d'ouvrages ou maîtres d'oeuvre, se réclament de la doctrine platonicienne des corps cosmiques, les cinq polyèdres réguliers, et ont fait du nombre d'or, "la divine proportion", un modèle de perfection esthétique et philosophique.
" L'Anneau des Mathématiques Francophones. Le nombre d'or. (Vitruve, architecte romain 1er siècle avant notre ère). Ainsi si a et b sont les deux grandeurs alors nous aurons : a/b = (a + b) / a. A/b = 1 + b/a pour simplifier, prenons comme variable x = a/b. alors nous obtenons : x = 1 + 1/x x - 1 - 1/x = 0 comme x non nul, nous obtenons l'équation suivante que nous noterons (E) : x2 - x - 1 = 0 qui admet comme racine positive : x = que nous notons Φ et vaut à peu près 1,618.... Le nombre d'or. L' histoire ...

Il y a 10 000 ans : Première manifestation humaine de la connaissance du nombre d'or (temple d'Andros découvert sous la mer des Bahamas). 2800 av JC : La pyramide de Khéops a des dimensions qui mettent en évidence l'importance que son architecte attachait au nombre d'or. Vè siècle avant J-C. (447-432 av.JC) : Le sculpteur grec Phidias utilise le nombre d'or pour décorer le Parthénon à Athènes, en particulier pour sculpter la statue d'Athéna Parthénos .
Il utilise également la racine carrée de 5 comme rapport. IIIè siècle avant J-C. : Euclide évoque le partage d'un segment en "extrême et moyenne raison" dans le livre VI des Eléments. 1498 : Fra Luca Pacioli, un moine professeur de mathématiques, écrit De divina proportione ("La divine proportion"). Au cours du XXème siècle : des peintres tels Dali et Picasso, ainsi que des architectes comme Le Corbusier, eurent recours au nombre d'or.
Nombre d'or. La proportion définie par a et b est dite d'« extrême et moyenne raison » lorsque a est à b ce que a + b est à a, soit : lorsque (a + b)/a = a/b. Le rapport a/b est alors égal au nombre d'or. Le nombre d'or (ou section dorée, proportion dorée, ou encore divine proportion) est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b), ce qui s'écrit : Le découpage d'un segment en deux longueurs vérifiant cette propriété est appelé par Euclide découpage en « extrême et moyenne raison ». Benoît Mandelbrot. Benoît Mandelbrot en 2007.
Il est le découvreur des fractales, nouvelle classe d'objets mathématiques, dont fait partie l'ensemble de Mandelbrot. Biographie[modifier | modifier le code] Cadre familial[modifier | modifier le code] Les Mandelbrot, originaires de Lituanie, habitent dans le quartier juif de Varsovie. Le père, Calel Mandelbrot, a suivi des cours à l'École de commerce, mais n'a pu poursuivre ses études universitaires à la suite de la naissance de son frère cadet, Szolem, dont il s'occupe après la mort de leur mère.
La famille maternelle de Benoît partage la même conception intellectuelle de la vie que sa famille paternelle et toutes deux l'inculquent à leurs enfants. Enfance et études[modifier | modifier le code] Le père de Benoît Mandelbrot fait la connaissance de Bertha, celle qui deviendra son épouse, pendant son enfance, car le frère aîné de celle-ci est un de ses camarades de classe. Fractale. Fractales On nomme fractale ou fractal (nom masculin moins usité), une courbe ou surface de forme irrégulière ou morcelée qui se crée en suivant des règles déterministes ou stochastiques.
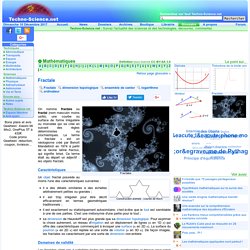
Le terme « fractale » est un néologisme créé par Benoît Mandelbrot en 1974 à partir de la racine latine fractus, qui signifie brisé. Fractales introduction. Fractale. Un article de Wikipédia, l'encyclopédie libre.
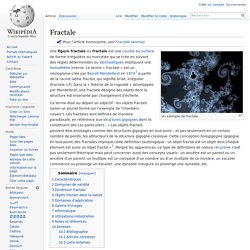
Ce terme était au départ un adjectif : les objets fractals (selon un pluriel formé sur l'exemple de "chantiers navals"). Les fractales sont définies de manière paradoxale, en référence aux structures gigognes dont ils constituent des cas particuliers : « Les objets fractals peuvent être envisagés comme des structures gigognes en tout point – et pas seulement en un certain nombre de points, les attracteurs de la structure gigogne classique. Cette conception hologigogne (gigogne en tout point) des fractales implique cette définition tautologique : un objet fractal est un objet dont chaque élément est aussi un objet fractal »[2].
Caractéristiques[modifier | modifier le code] Un objet fractal possède au moins l'une des caractéristiques suivantes : sa dimension de Hausdorff est strictement supérieure à sa dimension topologique. Domaines de validité[modifier | modifier le code] Les systèmes de fonctions itérées. (pour homothétie).