

Uncertainty principle. Where ħ is the reduced Planck constant.
The original heuristic argument that such a limit should exist was given by Heisenberg, after whom it is sometimes named the Heisenberg principle. This ascribes the uncertainty in the measurable quantities to the jolt-like disturbance triggered by the act of observation. Though widely repeated in textbooks, this physical argument is now known to be fundamentally misleading.[4][5] While the act of measurement does lead to uncertainty, the loss of precision is less than that predicted by Heisenberg's argument; the formal mathematical result remains valid, however. Since the uncertainty principle is such a basic result in quantum mechanics, typical experiments in quantum mechanics routinely observe aspects of it. Certain experiments, however, may deliberately test a particular form of the uncertainty principle as part of their main research program. Introduction[edit] Click to see animation. Wave mechanics interpretation[edit] . With yields. Pauli exclusion principle.
A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles.
This means that the wave function changes its sign if the space and spin co-ordinates of any two particles are interchanged. Zero-point energy. Zero-point energy, also called quantum vacuum zero-point energy, is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state.

All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature. The uncertainty principle requires every physical system to have a zero-point energy greater than the minimum of its classical potential well. This results in motion even at absolute zero.
For example, liquid helium does not freeze under atmospheric pressure at any temperature because of its zero-point energy. History[edit] Wave–particle duality. Origin of theory[edit] The idea of duality originated in a debate over the nature of light and matter that dates back to the 17th century, when Christiaan Huygens and Isaac Newton proposed competing theories of light: light was thought either to consist of waves (Huygens) or of particles (Newton).

Through the work of Max Planck, Albert Einstein, Louis de Broglie, Arthur Compton, Niels Bohr, and many others, current scientific theory holds that all particles also have a wave nature (and vice versa).[2] This phenomenon has been verified not only for elementary particles, but also for compound particles like atoms and even molecules. For macroscopic particles, because of their extremely short wavelengths, wave properties usually cannot be detected.[3] Brief history of wave and particle viewpoints[edit] Wave mechanics. Wave function. However, complex numbers are not necessarily used in all treatments.
Louis de Broglie in his later years proposed a real-valued wave function connected to the complex wave function by a proportionality constant and developed the de Broglie–Bohm theory. The unit of measurement for ψ depends on the system. For one particle in three dimensions, its units are [length]−3/2. Spin (physics) In quantum mechanics and particle physics, spin is an intrinsic form of angular momentum carried by elementary particles, composite particles (hadrons), and atomic nuclei.[1][2] Spin is a solely quantum-mechanical phenomenon; it does not have a counterpart in classical mechanics (despite the term spin being reminiscent of classical phenomena such as a planet spinning on its axis).[2]
Dirac equation. In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928.
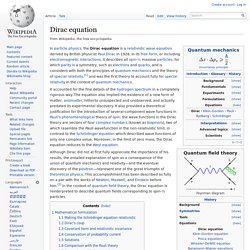
Schrödinger's cat. Schrödinger's cat: a cat, a flask of poison, and a radioactive source are placed in a sealed box.
If an internal monitor detects radioactivity (i.e. a single atom decaying), the flask is shattered, releasing the poison that kills the cat. The Copenhagen interpretation of quantum mechanics implies that after a while, the cat is simultaneously alive and dead. Yet, when one looks in the box, one sees the cat either alive or dead, not both alive and dead.
Quantum tunnelling. Quantum tunnelling or tunneling (see spelling differences) refers to the quantum mechanical phenomenon where a particle tunnels through a barrier that it classically could not surmount.
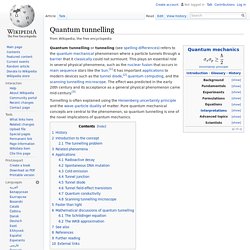
This plays an essential role in several physical phenomena, such as the nuclear fusion that occurs in main sequence stars like the Sun.[1] It has important applications to modern devices such as the tunnel diode,[2] quantum computing, and the scanning tunnelling microscope. The effect was predicted in the early 20th century and its acceptance as a general physical phenomenon came mid-century.[3] Quantum number. Quantum harmonic oscillator. Some trajectories of a harmonic oscillator according to Newton's laws of classical mechanics (A-B), and according to the Schrödinger equation of quantum mechanics (C-H).
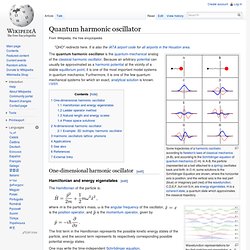
In A-B, the particle (represented as a ball attached to a spring) oscillates back and forth. In C-H, some solutions to the Schrödinger Equation are shown, where the horizontal axis is position, and the vertical axis is the real part (blue) or imaginary part (red) of the wavefunction. C,D,E,F, but not G,H, are energy eigenstates. Quantum entanglement. Quantum entanglement is a physical phenomenon that occurs when pairs or groups of particles are generated or interact in ways such that the quantum state of each particle cannot be described independently – instead, a quantum state may be given for the system as a whole.
Such phenomena were the subject of a 1935 paper by Albert Einstein, Boris Podolsky and Nathan Rosen,[1] describing what came to be known as the EPR paradox, and several papers by Erwin Schrödinger shortly thereafter.[2][3] Einstein and others considered such behavior to be impossible, as it violated the local realist view of causality (Einstein referred to it as "spooky action at a distance"),[4] and argued that the accepted formulation of quantum mechanics must therefore be incomplete.
History[edit] However, they did not coin the word entanglement, nor did they generalize the special properties of the state they considered. Concept[edit] Quantization (physics) The first method to be developed for quantization of field theories was canonical quantization. While this is extremely easy to implement on sufficiently simple theories, there are many situations where other methods of quantization yield more efficient procedures for computing quantum amplitudes.
Quantum. A photon is a single quantum of light, and is referred to as a "light quantum". The energy of an electron bound to an atom is quantized, which results in the stability of atoms, and hence of matter in general. As incorporated into the theory of quantum mechanics, this is regarded by physicists as part of the fundamental framework for understanding and describing nature at the smallest length-scales.
Etymology and discovery[edit] The word "quantum" comes from the Latin "quantus", for "how much". "Quanta", short for "quanta of electricity" (electrons) was used in a 1902 article on the photoelectric effect by Philipp Lenard, who credited Hermann von Helmholtz for using the word in the area of electricity. Beyond electromagnetic radiation[edit] See also[edit] References[edit] Further reading[edit] Operator (mathematics) Let U, V be two vector spaces. Any mapping from U to V is called an operator.
Let V be a vector space over the field K. Planck constant. Matrix mechanics. Identical particles. Identical particles, also called indistinguishable or indiscernible particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include, but are not limited to elementary particles such as electrons, composite subatomic particles such as atomic nuclei, as well as atoms and molecules. Quasiparticles also behave in this way. Although all known indistinguishable particles are "tiny", there is no exhaustive list of all possible sorts of particles nor a clear-cut limit of applicability; see particle statistics #Quantum statistics for detailed explication. There are two main categories of identical particles: bosons, which can share quantum states, and fermions, which do not share quantum states due to the Pauli exclusion principle. Hilbert space. Hamiltonian (quantum mechanics) Free particle. Correspondence principle.
Born–Oppenheimer approximation.