

Student Version - Instructor Evaluation Copy Request. Hexadecimal. Representation[edit] Written representation[edit] Using 0–9 and A–F[edit] In situations where there is no context, hexadecimal numbers can be ambiguous and confused with numbers expressed in other bases.
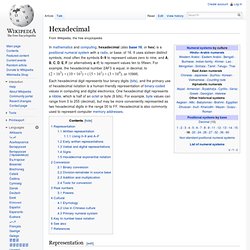
There are several conventions for expressing values unambiguously. A numerical subscript (itself written in decimal) can give the base explicitly: 15910 is decimal 159; 15916 is hexadecimal 159, which is equal to 34510. In linear text systems, such as those used in most computer programming environments, a variety of methods have arisen: There is no universal convention to use lowercase or uppercase for the letter digits, and each is prevalent or preferred in particular environments by community standards or convention.
Early written representations[edit] Bruce Alan Martin's hexadecimal notation proposal. Polynomial. The graph of a polynomial function of degree 3 Etymology[edit] According to the Oxford English Dictionary, polynomial succeeded the term binomial, and was made simply by replacing the Latin root bi- with the Greek poly-, which comes from the Greek word for many.
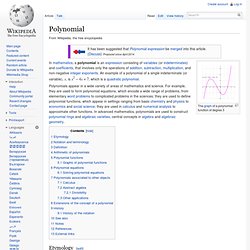
The word polynomial was first used in the 17th century.[1] Notation and terminology[edit] Duodecimal. The number twelve, a superior highly composite number, is the smallest number with four non-trivial factors (2, 3, 4, 6), and the smallest to include as factors all four numbers (1 to 4) within the subitizing range.
As a result of this increased factorability of the radix and its divisibility by a wide range of the most elemental numbers (whereas ten has only two non-trivial factors: 2 and 5, with neither 3 nor 4), duodecimal representations fit more easily than decimal ones into many common patterns, as evidenced by the higher regularity observable in the duodecimal multiplication table. As a result, duodecimal has been described as the optimal number system.[1] Of its factors, 2 and 3 are prime, which means the reciprocals of all 3-smooth numbers (such as 2, 3, 4, 6, 8, 9...) have a terminating representation in duodecimal.
Origin[edit] Languages using duodecimal number systems are uncommon. Blum axioms. In computational complexity theory the Blum axioms or Blum complexity axioms are axioms that specify desirable properties of complexity measures on the set of computable functions.
The axioms were first defined by Manuel Blum in 1967.[1] Importantly, the Speedup and Gap theorems hold for any complexity measure satisfying these axioms. The most well-known measures satisfying these axioms are those of time (i.e., running time) and space (i.e., memory usage). Definitions[edit] Partial function. Specifically, we will say that for any x ∈ X, either: f(x) = y ∈ Y (it is defined as a single element in Y) orf(x) is undefined.
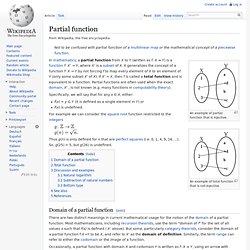
For example we can consider the square root function restricted to the integers Thus g(n) is only defined for n that are perfect squares (i.e. 0, 1, 4, 9, 16, ...). Analysis of algorithms. In computer science, the analysis of algorithms is the determination of the amount of resources (such as time and storage) necessary to execute them.
Most algorithms are designed to work with inputs of arbitrary length. Usually, the efficiency or running time of an algorithm is stated as a function relating the input length to the number of steps (time complexity) or storage locations (space complexity). Algorithm analysis is an important part of a broader computational complexity theory, which provides theoretical estimates for the resources needed by any algorithm which solves a given computational problem. These estimates provide an insight into reasonable directions of search for efficient algorithms. In theoretical analysis of algorithms it is common to estimate their complexity in the asymptotic sense, i.e., to estimate the complexity function for arbitrarily large input.
Radix. In mathematical numeral systems, the radix or base is the number of unique digits, including zero, that a positional numeral system uses to represent numbers.
For example, for the decimal system (the most common system in use today) the radix is ten, because it uses the ten digits from 0 through 9. In any numeral system (except unary, where radix is 1), the base will always be written as . Radix point. In English-speaking countries, the radix point is usually a small dot, ., placed either on the baseline or halfway between the baseline and the top of the numerals.
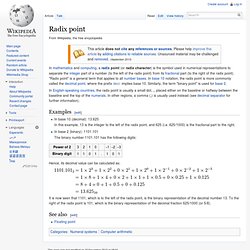
In other regions, a comma (,) is usually used instead (see decimal separator for further information). Examples[edit] In base 10 (decimal): 13.625. Leading zero. Occurrence[edit] Often, leading zeros are found on non-electronic digital displays[which?]
Or on such electronic ones as seven-segment displays, that contain fixed sets of digits. These devices include manual counters, stopwatches, odometers, and digital clocks. Leading zeros are also generated by many older computer programs when creating values to assign to new records, accounts and other files, and as such are likely to be used by utility billing systems, human resources information systems and government databases. Many digital cameras and other electronic media recording devices use leading zeros when creating and saving new files to make names of the equal length. Natural number. Natural numbers can be used for counting (one apple, two apples, three apples, ...)
In mathematics, the natural numbers are those used for counting ("there are six coins on the table") and ordering ("this is the third largest city in the country"). These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively (see English numerals). Significant figures. The significant figures of a number are those digits that carry meaning contributing to its precision. This includes all digits except: All leading zeros;Trailing zeros when they are merely placeholders to indicate the scale of the number (exact rules are explained at identifying significant figures); andSpurious digits introduced, for example, by calculations carried out to greater precision than that of the original data, or measurements reported to a greater precision than the equipment supports.
Significance arithmetic are approximate rules for roughly maintaining significance throughout a computation. The more sophisticated scientific rules are known as propagation of uncertainty. Numbers are often rounded to avoid reporting insignificant figures. Mathematical object. A mathematical object is an abstract object arising in philosophy of mathematics and mathematics.
Coefficient. The first two terms respectively have the coefficients 7 and −3. The third term 1.5 is a constant. Positional notation. Positional notation or place-value notation is a method of representing or encoding numbers. Math.com - World of Math Online. Everyday Math - Login. Www.tug.org/texshowcase/cheat. Fractal. Figure 1a. The Mandelbrot set illustrates self-similarity. As the image is enlarged, the same pattern re-appears so that it is virtually impossible to determine the scale being examined. Figure 1b. The same fractal magnified six times. Figure 1c. Figure 1d. Fractals are distinguished from regular geometric figures by their fractal dimensional scaling. As mathematical equations, fractals are usually nowhere differentiable.[2][5][8] An infinite fractal curve can be conceived of as winding through space differently from an ordinary line, still being a 1-dimensional line yet having a fractal dimension indicating it also resembles a surface.[7]:48[2]:15 There is some disagreement amongst authorities about how the concept of a fractal should be formally defined.
Introduction[edit] The word "fractal" often has different connotations for laypeople than mathematicians, where the layperson is more likely to be familiar with fractal art than a mathematical conception. History[edit] Figure 2. Computational complexity theory. Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other. Recursive definition. Four stages in the construction of a Koch snowflake.