

Golden-ratio. Fibonacci Numbers. Leonardo Fibonacci, sometimes called Leonardo of Pisa, was a thirteenth-century Italian mathematician.

He was instrumental in bringing the Arabic numbering system to Europe to replace the use of Roman numerals. He is also remembered for a series of numbers that now bears his name. The Fibonacci Sequence: Nature's Code. Nature, The Golden Ratio and Fibonacci Numbers. Plants can grow new cells in spirals, such as the pattern of seeds in this beautiful sunflower.
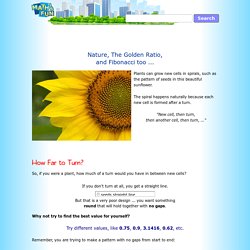
The spiral happens naturally because each new cell is formed after a turn. "New cell, then turn, then another cell, then turn, ... " How Far to Turn? So, if you were a plant, how much of a turn would you have in between new cells? Why not try to find the best value for yourself? Try different values, like 0.75, 0.9, 3.1416, 0.62, etc. Remember, you are trying to make a pattern with no gaps from start to end: (By the way, it doesn't matter about the whole number part, like 1. or 5. because they are full revolutions that point us back in the same direction.) What Did You Get? The Golden Ratio in Nature"
You won't find Fibonacci numbers everywhere in the natural world -- many plants and animals express different number sequences.
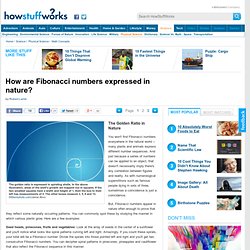
And just because a series of numbers can be applied to an object, that doesn't necessarily imply there's any correlation between figures and reality. As with numerological superstitions such as famous people dying in sets of three, sometimes a coincidence is just a coincidence. But, Fibonacci numbers appear in nature often enough to prove that they reflect some naturally occurring patterns. You can commonly spot these by studying the manner in which various plants grow. Here are a few examples: Seed heads, pinecones, fruits and vegetables: Look at the array of seeds in the center of a sunflower and you'll notice what looks like spiral patterns curving left and right.
Flowers and branches: Some plants express the Fibonacci sequence in their growth points, the places where tree branches form or split. Fabulous Fibonacci Fun! Fibonacci Sequence. This sequence is named after the Italian mathematician who lived during the 12th century.

It occurs in nature, modelling the population growth in rabbits, and also the development of the spiral in a snail's shell. The terms in the sequence can be made by adding the previous two terms: There is a worksheet here, which can be printed and photocopied for children to use. It involves the children trying to work out how the sequence is made, and then getting them to work out the first 25 numbers in the sequence. These are listed below...
The children may want to use a calculator to carry out the latter part of the exercise, but whether they use one or not, they should understand the importance of being accurate (and checking their calculations for errors). How are Fibonacci numbers expressed in nature. Is there a magic equation to the universe?

A series of numbers capable of unraveling the most complicated organic properties or deciphering the plot of "Lost"? Probably not. But thanks to one medieval man's obsession with rabbits, we have a sequence of numbers that reflect various patterns found in nature. In 1202, Italian mathematician Leonardo Pisano (also known as Fibonacci, meaning "son of Bonacci") pondered the question: Given optimal conditions, how many pairs of rabbits can be produced from a single pair of rabbits in one year? This thought experiment dictates that the female rabbits always give birth to pairs, and each pair consists of one male and one female.
Think about it -- two newborn rabbits are placed in a fenced-in yard and left to, well, breed like rabbits. Fibonacci. Doodling in Math: Spirals, Fibonacci, and Being a Plant [1 of 3] Fibonacci for Kids! The Numbers of Nature - Amazing Math Video. Fibonacci Sequence. The Fibonacci Sequence is the series of numbers: The next number is found by adding up the two numbers before it.

The 2 is found by adding the two numbers before it (1+1) Similarly, the 3 is found by adding the two numbers before it (1+2), And the 5 is (2+3), and so on! Example: the next number in the sequence above is 21+34 = 55 It is that simple! Here is a longer list: Can you figure out the next few numbers? Makes A Spiral When we make squares with those widths, we get a nice spiral: Do you see how the squares fit neatly together? The Rule The Fibonacci Sequence can be written as a "Rule" (see Sequences and Series). First, the terms are numbered from 0 onwards like this: So term number 6 is called x6 (which equals 8). Microsoft Word - Fibonacci WEB.doc - mfklessons-fibonacci-all.pdf.