

Figures de jonglage avec les boites à cigares. Le cirque dans l'art pictural. Le cirque des artistes peintres Karel Appel Bernard Buffet Fernando Botero Alexander Calder Marc Chagall Robert Combas Geneviève Peyrade Fernand Léger Henri Matisse Francis Picabia Pablo Picasso Pierre-Auguste Renoir Georges Rouault Hugo Scheiber Georges Seurat Gustave De Smet James Tissot Henri de Toulouse-Lautrec Si vous connaissez d'autres œuvres, n'hésitez pas, je suis preneuse!
ICI, vous retrouvez toutes mes compilations de tableaux. Les Objets Volants. Une aventure jonglistique Au milieu des années 80 est apparu un modèle mathématique du jonglage, s'appuyant sur les temps de trajet des objets dans une figure.
Le temps de trajet d'un objet est décrit par un nombre; une figure est donc décrite par une suite de nombres, sur laquelle des calculs peuvent s'effectuer pour déduire de nouvelles figures. Ce modèle mathématique, appelé siteswap, est devenu une notation très pratique et à la portée de chacun, mais aussi un puissant outil d'exploration. Jonglage.pdf. Jonglage et jonglerie avec balles - Siteswap. Le Siteswap(ou les mathématiques du jonglage) Sommaire: Bref historiquePourquoi le Siteswap?
Principes de base Notation basique Simplification Décortication de la figure Cas particuliers : transfert, balle gardée et main videPropriétés du siteswapValidation d’une séquence siteswapComment vérifier si une séquence est valide? Siteswap et 3 ballesSiteswap et figures multiplexSiteswap et figures synchronesDouches et cascades: une même familleQuelques exemples de figures en siteswap Bref historique C’est en 1985 que 3 américains et 1 anglais (Bruce Tiemann (*), Bengt Magnusson, Paul Klimek, et Mike Day) passionnés de jonglerie et/ou de mathématiques eurent l’idée de créer un langage spécifique à cette discipline qui devait permettre de codifier simplement toute figure de jonglage. (*) Bruce Tiemann dit " Boppo " de l’université du Collorado réalise un étonnant flash 11 balles. Siteswap. Historique de la notation[modifier | modifier le code] La liste de diffusion rec.juggling en activité depuis août 1990 sur Usenet[2] et les débuts d’Internet permirent la diffusion rapide de ces notions parmi la communauté des jongleurs scientifiques. rec.juggling reste aujourd’hui la source d’information la plus complète sur le siteswap : premiers diagrammes états-transitions, annonce et souvent publication de l’essentiel des travaux mathématiques liés à la notation ainsi que de nombreux conseils pour les jongleurs dans la pratique.
Les bases : le siteswap asynchrone[modifier | modifier le code] Pour décrire la séquence, on détermine pour chaque étape combien de temps plus tard l’objet sera relancé. Le nombre associé à chaque lancer permet de déterminer le nombre de temps que la balle passera en l’air et ainsi d’évaluer la hauteur relative du lancer. C’est pourquoi beaucoup interprètent les nombres comme des hauteurs : Model Behavior: The Mathematics of Juggling. The late computer scientist Claude Shannon has a well-deserved reputation as the father of information theory, but he was also an avid unicyclist, juggler and tinkerer.
He even built his own robotic juggling machine out of parts from an Erector set, programming it to juggle three metal balls by bouncing them against a drum. In the early 1980s, Shannon published the first formal mathematical theorem of juggling, correlating the length of time balls are in the air with how long each ball stays in the juggler’s hand. Images des mathématiques. 11 juillet 2009 - Rédigé par Stéphane Lamy Ceux qui lisent attentivement mes billets savent déjà que je pratique depuis assez longtemps le jonglage...
Pour situer mon niveau d’amateur éclairé, j’ai l’habitude de dire que je ne me suis jamais retrouvé dans un tel état d’ébriété que je n’aurais plus été capable de jongler à 5 balles (ceci dans le but transparent de me faire immédiatement payer des coups à boire par l’auditoire sceptique). Collège Mignet - Classes Cirque. Amis Circassiens, Pour la quatrième année consécutive, une classe à projet : « Autour des Arts du Cirque » est reconduite au collège Mignet à la rentrée 2014 pour les classes de 6e2, 5e2, 4è 2 et 3ème 2.

Le projet, à la fois culturel et artistique, se propose d’utiliser le Cirque comme support pédagogique aux apprentissages dans différentes disciplines : Education physique et sportive : développement artistique, acrobatique,culturel, et citoyen avec un travail en équipe autour d’un projet commun. La classe Cirque organise également une grande collecte de petits bouchons au profit de Handi’chiens ( Espace Pédagogique : action culturelle - mathématiques et arts plastiques : autour du cirque dans un collège (53) Cela vaut aussi pour les quatrièmes.PRESENTATION DE L'ACTIVITE : réaliser un petit chapiteau en papier cartonné, tout en travaillant sur la base de la symétrie axialeBUT DE L'ACTIVITE : compléter un patron à l'aide de deux symétries axiales successives et construire ce chapiteau.
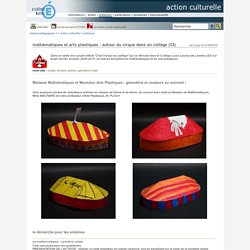
(le patron se trouve au bas de cette page)DEROULEMENT DE L'ACTIVITE : chaque élève avait en sa possession le quart d'un patron de chapiteau de cirque. Il devait réaliser deux symétries axiales successives pour obtenir le patron complet.Ceci fait, il ne restait plus qu'à découper le patron et à construire le chapiteau.DIFFICULTES EVENTUELLES : les élèves ont besoin de voir un chapiteau terminé, pour visualiser le résultat fini et mieux comprendre le montage.Souvent peu précis, ils ont vraiment besoin d'être accompagnés des professeurs.
Cirque et mathématiques, une équation résolue au collège Pierre Brossolette.