

Peinture. - La règle du nombre d'or - Connu depuis la Grèce antique, le nombre d’or vaut (1+√5)/2, c’est à dire approximativement 1,61803398875.
Il est utilisé pour définir des proportions harmonieuses en géométrie, et a même été qualifié de divine proportion, notamment pendant la Renaissance. Le nombre d’or est actuellement représenté par la lettre phi (φ). Un des plus beaux exemples de la mise en application de la règle du nombre d’or est le Parthénon situé sur l’Acropole d’Athène, mais cette divine proportion est également très présente dans la nature.
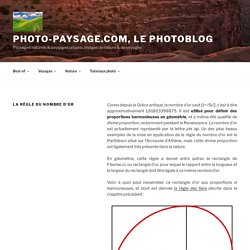
En géométrie, cette règle a donné entre autres le rectangle de Fibonacci, ou rectangle d’or, pour lequel le rapport entre la longueur et la largeur du rectangle doit être égale à ce même nombre d’or. Voici à quoi peut ressembler ce rectangle d’or aux proportions si harmonieuses, et dont est dérivée la règle des tiers décrite dans le chapitre précédent : NOMBRE D'OR - FORMATS TABLEAUX - LES BASES DU DESSIN ... et de la PEINTURE. Peinture. LE NOMBRE D'OR - atelier portrait pastel aquarelle visages dessin regard. La loi du nombre d'Or ou "divine proportion" correspond à une proportion harmonieuse.
Symbole d'harmonie et de beauté universelle. Présente dans divers monuments anciens : pyramides, temples grecs, cathédrales gothiques. En peinture, la loi du nombre d'Or sert à calculer les proportions idéales pour la composition et l'harmonie d'un tableau. La première utilisation connue du nombre d'Or est due au sculpteur grec Phidias (490-430 avant JC). Pour les artistes, qu'ils soient peintres, sculpteurs, dessinateurs ou architectes, le nombre d'Or est défini ainsi : "Pour qu'un espace divisé en parties inégales apparaisse agréable et esthétique, il devra exister entre la plus petite et la plus grande partie la même relation qu'entre cette dernière et l'ensemble".
Etude d'un tableau et nombre d'or - Site d'Histoire Des Arts. Le nombre d’or en peinture Étude d’un tableau : le Sacrement de la dernière Cène, de Salvador DALI A la découverte d’un nombre et de ses propriétés à travers l’étude d’un tableau Quelques pistes pour préparer l’HDA (si tu choisis ce sujet)Une autre œuvre de Salvador Dali construite avec le nombre d’or BONUS : Pistes de réflexions pour réaliser une œuvre personnelle Le nombre d’or en musique Michael Blake étant un amoureux de la musique et des mathématiques, il s’est illustré avec le nombre Pi, et le voilà de retour avec Phi (ou aussi Tau) aussi appelé nombre d’or et qui vaut approximativement 1.618033989.

Le nombre d’or en poésie Un exemple, Le serpent qui danse, de Charles Baudelaire. Lecture du poème : Le serpent qui danse, de Charles Baudelaire. Le Nombre d'Or - Histoire. Le nombre d'or dans la peinture, l'architecture et la nature - Le Nombre D'or. De nos jours, nous pouvons dire qu’il existe deux types de nature : la nature végétale et la nature animal.

En les examinant de plus près nous pouvons remarquer que toutes deux peuvent présenter la suite de Fibonacci ainsi que les proportions d’Euclide. De ce fait, nous pouvons dire que le nombre d’or est présent partout dans la nature. La suite de Fibonacci fut créée par un célèbre mathématicien italien : Leonardo Fibonacci au XII ème siècle. Cette suite commence par 0 et 1 (ses deux premiers termes). A partir du rang numéro 2, il suffit d’additionner les deux termes précédents afin de trouver les termes suivants. A travers cette démonstration, nous allons prouver le lien existant entre la suite de Fibonacci et le nombre d’or. Nous avons vu précédemment que la suite de Fibonacci était définie à partir de 0 et 1. Nous pouvons alors poser la relation suivante avec n appartenant à l'ensemble d'entiers naturels (grâce à la définition de la suite de fibonacci exprimé ci-dessus) : Δ= b²- 4ac. L'utilisation du nombre d'or chez Enguerrand Quarton. E.

Quarton, une des grandes figures de la peinture française du XVe siècle. Originaire du diocèse de Laon en Picardie, Enguerrand Quarton ne nous est connu que par son activité en Provence, attestée de 1444 à 1466.