

1,2,3,4,5,6,7,8,9 et zéro sont appelés chiffres arabes. Qui les a inventés? Cauty06_nombres. André Cauty, Professeur des Universités à Bordeaux 1, équipe CELIA du CNRS Article déposé le 16 juin 2006.

Toute reproduction pour publication ou à des fins commerciales, de la totalité ou d'une partie de l'article, devra impérativement faire l'objet d'un accord préalable avec l'éditeur (ENS Ulm). Toute reproduction à des fins privées, ou strictement pédagogiques dans le cadre limité d'une formation, de la totalité ou d'une partie de l'article, est autorisée sous réserve de la mention explicite des références éditoriales de l'article. Importer l'article en version pdf - Ecrire à l'auteur. Histoire des nombres** Dès la création de la numérologie, le système binaire s'impose et l'informatique d'aujourd'hui n'est qu'un étrange retour aux sources !

Les historiens des nombres comme Georges Ifrah (Histoire universelle des chiffres) ne s'intéressent qu'au plan strictement mathématique. Ils passent sous silence, que la science des nombres des anciens est avant tout une science du sacré. Avant d'être un signe, le chiffre est avant toute une vision de la perception du monde.
Il est un concept exposant le plan divin. Qui dit plan dit nécessairement géométrie divine. L'histoire des chiffres. Figuration des nombres chez les Hébreux et les Grecs.Chez les Hébreux, les nombres sont figurés par des lettres et, de deux lettres, celle de droite représente la valeur la plus élevée; les mille, dizaines et centaines de mille seront représentés par les mêmes caractères, surmontés de deux points.
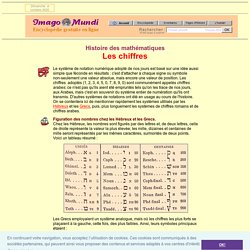
Voici un tableau résumé :- Les Grecs employaient un système analogue, mais où les chiffres les plus forts se plaçaient à la gauche, cette fois, des plus faibles. Ainsi, leurs symboles principauxétaient :-- Cependant, les Grecs n'avaient pas de système homogène : les myriades (c'est-à-dire les dix-mille) pouvaient se noter de plusieurs façons différentes; parfois, ils utilisaient les grandes lettres avec une manière de chiffrer analogue à celle des Romains. Histoire de(s) nombres. Histoire de(s) nombres Ecriture des nombres Les premiers nombres utilisés furent les nombres entiers : ils servaient à compter les objets, les troupeaux, les individus.

Les premières traces de comptage connues sont les os entaillés des chasseurs du paléolithique (environ 15 000 avant J.C.) Un système d’écriture des nombres s’appelle une numération. Les chiffres sont les symboles qui servent à écrire les nombres. Dans une numération dite de position, un chiffre peut avoir une valeur différente selon sa place dans l’écriture d’un nombre. Exemple : 333 Numération babylonienne (Mésopotamie vers 1800 av. Les babyloniens utilisaient une numération de position de base soixante, n’utilisant que deux chiffres : le chevron et le clou. A - Histoire des Nombres. Un tableau synoptique sur l'histoire des nombres. L'humanité a mis des millénaires pour passer de la quantité aux nombres. L'idée de nombre est l'aboutissement d'un long travail d'abstraction de la pensée. -30 000.Présence d'entailles numériques.- 8 000.Apparition des calculi au Moyen Orient.-3 300.Premiers chiffres à Sumer et en Elam.
Première numérotation écrite.Naissance de l'écriture.-2 700.Chiffres sumériens cunéiformes.-2 000.Apparition de la base décimale.-1 800.Numérotation babylonienne savante. Histoire des nombres. L'histoire des mathématiques est précédée d'une longue préhistoire dont nous avons des traces remontant à 4000 ans.

Les animaux supérieurs, les jeunes enfants perçoivent dans notre monde deux entités abstraites fondamentales : le nombre et la forme. L'arithmétique et la géométrie furent ainsi, longtemps distinctes, les deux sciences fondamentales. Au départ la connaissance des nombres chez l'homme n'est pas très fine. L'homme, dans les sociétés primitives, ne distingue pas deux ensembles équipotents, il sait à peine compter : un, deux, beaucoup. "Beaucoup" se dit "tres" en latin : ce mot subsiste encore aujourd'hui en français : "très" mais aussi "trois"! L'Histoire des Nombres : Le Chiffre. L'Histoire des Nombres : Le Chiffre. 1) Les chiffres Egyptiens En Egypte, en l'an 3500 avant notre ère, la notation des chiffres était basée, comme l'écriture, sur les hiéroglyphes.

Chaque signe possédait une valeur, tel que:L'unité était représentée par une barre verticale, 10 par une anse, 100 par une boucle, les milliers par une fleur de Lotus, 10 000 par un doigt vertical légèrement recourbé, 100 000 par un têtard et le million par un humain aux bras levés : Les chiffres ci-dessous qui doivent être lus à la fois verticalement et horizontalement, signifient 1 234 567.Ils appartiennent à ce que nous appelons l'écriture hiéroglyphique, celle des initiés. Avant d'avoir trouvé l'utilisation du papyrus, les Egyptiens transcrivaient leurs signes dans la cire : Pratiques et mathématiques combinatoires en Chine (2) Maître de conférences, Université Lille I, Laboratoire Paul Painlevé UMR CNRS 8524, chercheur associé du REHSEIS - UMR7596 (page web) Le texte de Wang Lai (1768-1813) Cet auteur est bien connu des spécialistes pour avoir été membre de l’école philologique Qian-Jia [1] et pour avoir conduit des travaux en algèbre traditionnelle.

Cependant son essai Les principes mathématiques des combinaisons successives (Dijian shuli 遞兼數理) [2] reste, lui, méconnu. D’un point de vue mathématique moderne, les « combinaisons successives » de Wang Lai sont les coefficients binomiaux C_n^k. Ils correspondent au nombre de combinaisons possibles lorsqu’on tire (sans remise) k objets parmi n. Regardons tout d’abord la structure de ce texte qui comporte une dizaine de pages. \sum_{k=1}^{n}k=\frac{n (n+1)}{1\cdot 2}, \sum_{k=1}^{n}\frac{k (k+1)}{1 \cdot 2}=\frac{n(n+1)(n+2)}{1\cdot 2\cdot 3}, \ldots Entrons dans le détail. CHINE : Maths-rometus, Mathématiques chinoises, Civilisation mathématicienne, Histoire des maths, Maths, Mathématiques, Math, Jean-Luc Romet. Dans le livre de mathématiques "Chiu Chang", qui date du Ier siècle après JC, on trouve : des additions et soustractions de fractions et des pourcentages pour l'arpentage ; des suites de nombres et la règle de trois pour les distributions proportionnelles ; des racines carrées et cubiques pour les mesures des champs ; des volumes de solides dans un texte pour les ingénieurs ; des résolutions de systèmes d'équations à deux inconnues ; des problèmes sur la longueur des côtés d'un triangle rectangle.
Histoire de Nombres, Histoire de machines à calculer. Collège Arthur Rimbaud Marseille - Histoire des maths. CHIFFRES : Maths-rometus, Etymologie des chiffres, Histoire du zéro, Graphisme, Symbolisme, Numérologie, Mathématiques, Maths, Math, Jean-Luc Romet. 4) Le graphisme de nos chiffres Voici un moyen mnémotechnique que les auteurs pendant la Renaissance avaient imaginé pour faire retenir les graphismes des chiffres. On trace autant de segments que le chiffre l'indique. Selon une tradition populaire, encore tenace en Égypte et en Afrique du Nord, la version moderne de nos chiffres "indo-arabes" serait l'invention d'un vitrier-géomètre originaire du Maghreb, qui aurait imaginé de donner aux neuf chiffres significatifs une forme dépendant du nombre des angles contenus dans le dessin de chacun d'eux :un angle pour le chiffre 1, deux angles pour le chiffre 2, etc...Tout ceci n'est bien sûr que supposition.
Éclairage cognitif sur la complexité de différents systèmes de numération. Pour entrer dans le sujet, je voudrais faire un petit tour dans les dictionnaires, histoire de baliser le terrain. Les mathématiciens parmi vous voudrons bien m’excuser, mais ma pratique de cet objet conceptuel particulier qu’est le nombre est vraiment très instinctive.
J’utilise les nombres comme des outils aussi puissants et aussi naturels que le sont mes mains, et je ne me suis jamais posé de questions métaphysiques à leur propos. J’ai donc entrepris l’exercice bizarre qui consiste à chercher des définitions pour comprendre cette évidence qu’est le nombre. Le résultat est intriguant. Si on écarte les tentatives de définitions tautologiques du genre « le nombre est la notion qui permet de dénombrer des choses » (Larousse !) Pour essayer d’y voir plus clair, je me suis rabattu sur le terme « numération » et, à voir la définition, j’en ai conclu que je n’étais pas le premier à faire ce chemin. Le concept de représentation est central en psychologie cognitive.
Systèmes 1D Systèmes 1x1D et.