Fibonacci

Vidéo - Fabonacci

Fibonacci. Leonardo Bonacci (c. 1170 – c. 1250)[2]—known as Fibonacci (Italian: [fiboˈnattʃi]), and also Leonardo of Pisa, Leonardo Pisano, Leonardo Pisano Bigollo, Leonardo Fibonacci—was an Italian mathematician, considered as "the most talented Western mathematician of the Middle Ages.

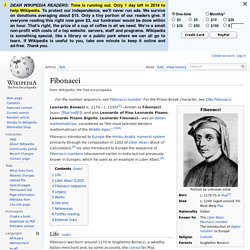
".[3][4] Fibonacci introduced to Europe the Hindu–Arabic numeral system primarily through his composition in 1202 of Liber Abaci (Book of Calculation).[5] He also introduced to Europe the sequence of Fibonacci numbers (discovered earlier in India but not previously known in Europe), which he used as an example in Liber Abaci.[6] Life[edit] Biographie : Leonardo Fibonacci (1170 [Pise] - 1245 [Pise]) Leonard de Pise, plus connu sous le nom de Fibonacci, est le premier grand mathématicien de l'ère chrétienne du monde occidental.

D'assez nombreux détails de sa jeunesse nous sont connus par les propos qu'il tient lui-même dans la préface d'un de ses livres, le Liber abaci. Né à Pise vers 1170, il rejoint très jeune son père à la colonie de Bujania, en Algérie, où ce dernier est responsable du bureau des douanes pour le compte de l'ordre des marchands de Pise. Voulant faire de son fils un marchand, il l'initie à l'art du calcul indo-arabe. Fibonacci apprendra en outre les savoirs et algorithmes orientaux grâce à ses nombreux voyages en Syrie, en Grèce, en Egypte. Vers 1200, il retourne vivre dans sa ville natale (où il verra la construction de la célèbre tour penchée). Fibonacci vivait avant l'invention de l'imprimerie, ce qui signifiait que pour avoir plusieurs exemplaires du même ouvrage, il fallait le travail entièrement manuel d'un copiste.

Leonardo Fibonacci. Un article de Wikipédia, l'encyclopédie libre.

Leonardo Fibonacci Statue de Léonard de Pise, dans sa ville natale Leonardo Fibonacci (v. 1175 à Pise, Italie - v. 1250) est un mathématicien italien. Il avait, à l'époque, pour nom d'usage « Leonardo Pisano » (il est encore actuellement connu en français sous l'équivalent « Léonard de Pise »), et se surnommait parfois lui-même « Leonardo Bigollo » (bigollo signifiant « voyageur » en italien). Biographie[modifier | modifier le code] Né à Pise en Italie, son éducation s'est faite en grande partie à Béjaïa en Algérie, où son père Guilielmo Bonacci était le représentant des marchands de la république de Pise.

Résumé Fibonacci. Suite de Fibonacci. Un article de Wikipédia, l'encyclopédie libre.

Elle doit son nom à Leonardo Fibonacci qui, dans un problème récréatif posé dans l'ouvrage Liber abaci publié en 1202, décrit la croissance d'une population de lapins : « Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ? » Cette suite est fortement liée au nombre d'or, φ (phi). Ce nombre intervient dans l'expression du terme général de la suite. Croissance de population des lapins selon une suite de Fibonacci Présentation mathématique[modifier | modifier le code] Formule de récurrence[modifier | modifier le code] Le problème de Fibonacci est à l'origine de la suite dont le -ième terme correspond au nombre de paires de lapins au -ème mois. Notons le nombre de couples de lapins au début du mois .

Plaçons-nous maintenant au mois désigne la somme des couples de lapins au mois et. Nombre d'or, suite de Fibonacci et autres grilles de mise en page pour le design web. Suite de Fibonacci. The Fibonacci Sequence is the series of numbers: The next number is found by adding up the two numbers before it.

The 2 is found by adding the two numbers before it (1+1) Similarly, the 3 is found by adding the two numbers before it (1+2), And the 5 is (2+3), and so on! Example: the next number in the sequence above is 21+34 = 55 It is that simple! Here is a longer list: Can you figure out the next few numbers? Makes A Spiral When we make squares with those widths, we get a nice spiral: Do you see how the squares fit neatly together?

Fibonacci Numbers, the Golden section and the Golden String. Fibonacci number. A tiling with squares whose side lengths are successive Fibonacci numbers.

Codage de Fibonacci. Un article de Wikipédia, l'encyclopédie libre.

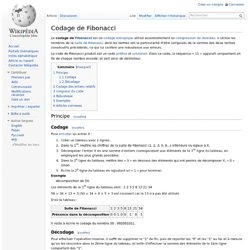
Le codage de Fibonacci est un codage entropique utilisé essentiellement en compression de données . Il utilise les nombres de la suite de Fibonacci , dont les termes ont la particularité d'être composés de la somme des deux termes consécutifs précédents, ce qui lui confère une robustesse aux erreurs. Le code de Fibonacci produit est un code préfixe et universel . Dans ce code, la séquence « 11 » apparaît uniquement en fin de chaque nombre encodé, et sert ainsi de délimiteur. Principe [ modifier ] Codage [ modifier ] Pour encoder un entier X : Créer un tableau avec 2 lignes. Exemple décomposition de 50. Les éléments de la 1 re ligne du tableau sont : 1 2 3 5 8 13 21 34 50 = 34 + 13 + 3 (50 = 34 + 8 + 5 + 3 est incorrect car le 13 n'a pas été utilisé) D'où le tableau : Il reste à écrire le codage du nombre 50 : 001001011. Fibonacci, Carroll, lapin. Suite de nombres dont chaque terme est la somme des deux précédents:

Valeurs des 5000 premiers termes de la suite de fibonacci. The Fibonacci Numbers and Golden section in Nature - 1. This page has been split into TWO PARTS.

This, the first, looks at the Fibonacci numbers and why they appear in various "family trees" and patterns of spirals of leaves and seeds. The second page then examines why the golden section is used by nature in some detail, including animations of growing plants. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 1 Rabbits, Cows and Bees Family Trees Let's look first at the Rabbit Puzzle that Fibonacci wrote about and then at two adaptations of it to make it more realistic. Les retracements de Fibonacci : Analyse technique. Vous avez surement un jour entendu parlé de la suite de Fibonacci, rappelez vous : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …… Pour les obtenir c’est très simple.

Vous additionnez les deux premiers chiffres pour calculer le 3eme. Ainsi 1+1=2 ;1+2=3 ;2+3=5… quelques souvenirs vous reviennent ? Venons en aux nombres d’or maintenant. Le nombre d’or est le rapport entre deux chiffres compris dans cette suite. Tout d’abord on calcule le ratio entre un nombre et son suivant par exemple, 89/144=0.618. Les retracements de Fibonacci : Parlons maintenant de ce pourquoi vous êtes venus, les niveaux de retracements de Fibonacci : 23,6%, 38,2%, 50,0%, 61.8%, 100% . - Une tendance haussière est marquée par des phases de corrections - Une tendance baissière est marquée par des phases de rebonds.

Ce sont ces corrections ou rebonds qui sont appelés des retracements. Pour le retracement 38.2%, vous ferez le calcul suivant : 1.4110 - (0.0100 * 38.2%) = 1.4072.