

Hindging a Moebius Strip Kangaroo. That's amazing Daniel!
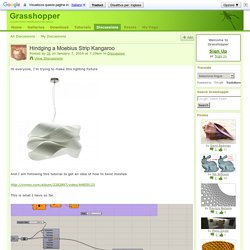
Thank you! If you don't mind, could you explain a few things? I tried to recreate your definition, but for some reason I get this gap. Mobius strip in Grasshopper (RO) Relaxation + Remeshing with Plankton and Kangaroo. Kangaroo - Mesh Relaxation - Tutorial 3. Kangaroo - Mesh Relaxation - Tutorial 2. Kangaroo - Mesh Relaxation - Tutorial 1. Mesh relaxing with kangaroo. Grasshopper code. . a collection of codes & grammars for Grasshopper, a generative modeling tool for Rhinoceros. 3D Hilbert Curve This definition generates a 3D Hilbert Curve, a continuous fractal space-filling curve. 3D_Hilbert_Curve_Co-de-iT_1.0007.zip nGon mesh tessellation Starting from a closed surface it builds a nGon mesh tessellation nGon_tessellation_Co-de-iT_1.0007.zip Curves Sorter Starting from a list of curves it takes the first one then it looks for the closest curve and it eventually flips the direction to optimize the toolpath lenght.

Curves_Sorter_Co-de-iT_1.0007.zip froGH A sparse collection of tools for Grasshopper. See the code, explanation and download here. Clusterizer This definition groups indexes of connected points into separate clusters. Clusterizer_Co-de-iT_0.9.0076.zip Spirograph. Fig. 13: Decomposition results of a saddle-shaped surface using... - Scientific Figure on ResearchGate. Education/Grasshopper. Code of Space. The current events and Grasshopper workshops you could find in PARAMETRIC EVENTS.
Python General/basics: Python in Rhino/Grasshopper: Autodesk DYNAMO – add-on for Building Information Modeling in Revit: dynamoprimer.com. New tutorial - Developable strips - Part 3. Following on from parts 1 & 2 Once we have relaxed our mesh, and stopped the timer, we can click the Data Dam to pass the result to the next part of the definition: The Stripper* component breaks the mesh into long strips 1 quad wide.
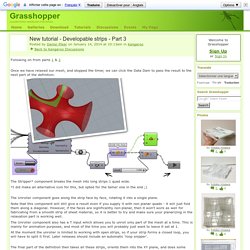
*I did make an alternative icon for this, but opted for the tamer one in the end ;) The Unroller component goes along the strip face by face, rotating it into a single plane. Note that this component will still give a result even if you supply it with non planar quads - it will just fold them along a diagonal. New tutorial - Developable strips - Part 1. A while ago I posted this video about generating and unrolling developable strips: Today I'm going to explain how to set this up in Kangaroo.
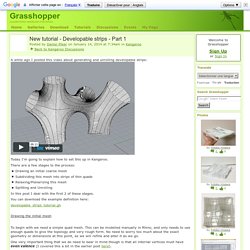
There are a few stages to the process: Drawing an initial coarse meshSubdividing this mesh into strips of thin quadsRelaxing/Planarizing this meshSplitting and Unrolling In this post I deal with the first 2 of these stages. You can download the example definition here: developable_strips_tutorial.gh Drawing the initial mesh To begin with we need a simple quad mesh. One very important thing that we do need to bear in mind though is that all internal vertices must have even valence (I covered this a bit in the earlier post here). So for example, this is bad: (because the highlighted vertex is surrounded by 5 faces) While this is good (and can still be relaxed to the same shape): (the top and bottom vertices have valence 8, and the vertices between the arms have valence 4) The reasons why we need this condition should become more clear in the later steps.
Minimal surfaces. Frequently occuring in nature, minimal surfaces are defined as surfaces with zero mean curvature.

These surfaces originally arose as surfaces that minimized total surface area subject to some constraint. Physical models of area-minimizing minimal surfaces can be made by dipping a wire frame into a soap solution, forming a soap film, which is a minimal surface whose boundary is the wire frame. The thin membrane that spans the wire boundary is a minimal surface of all possible surfaces that span the boundary, it is the one with minimal energy. One way to think of this “minimal energy” is that to imagine the surface as an elastic rubber membrane: the minimal shape is the one that in which the rubber membrane is the most relaxed. A minimal surface parametrized as x=(u,v,h(u,v)) therefore satisfies Lagrange`s equation (1+h(v)^2)*h(uu)-2*h(u)*h(v)*h(uv)+(1+h(u)^2)*h(vv)=0 (Gray 1997, p.399)
Mesh Relaxation component. My first release of a Grasshopper component.
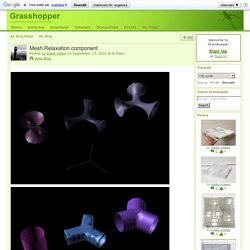
A mesh relaxation component based on a force density algorithm. The component used a mesh, rather than a brep, determines it's naked (lose) edges and relaxes the mesh nodes. All of this woudnt be possible without the inspiration and some components from: - Jon Mirtschin : / - Ursula Frick & Thomas Grabner: - Giulio Piacentino : it's Weaverbird component: Some of the examples and scripts i have included in the package use Giulio Piacentino's Weaverbird and uto's mesh tools. please be sure to have them installed for the script to properly work. Before downloading the package please be advised that is protected by a licence. Creative Commons: Attribution-NonCommercial-ShareAlike 3.0 Romania | And the package can be downloaded here.
Already at version 1.01 - be sure to redownload it if you only have one component. Mesh Relaxation Study.